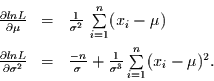

Nächste Seite: Bayes-Schätzer
Aufwärts: Schätzverfahren
Vorherige Seite: Methode der kleinsten Quadrate
Maximum-Likelihood-Schätzer (ML-Schätzer, nach Fisher, 1890 - 1962) basieren
auf der Annahme, daß wahrscheinlich das Wahrscheinlichste wahr ist. Das
klingt hoffentlich schon so, daß der kritische Leser, auf den Gedanken kommen
könnte, daß die damit erzielten Ergebnisse auch total falsch sein
können. Trotzdem neigt man auch im Alltag gerne dazu, nach diesem Prinzip zu
schätzen. Weiß man von einem Koch z.B. daß er wesentlich wahrscheinlicher
eine Suppe versalzt, wenn er verliebt ist, als wenn er es nicht ist, so wird
man sich während dem Essen einer versalzenen Suppe denken: ``wahrscheinlich
ist der Koch (mal wieder) verliebt``. Genau das ist eine ML-Schätzung.
Um ML-Schätzungen durchführen zu können, braucht man eine
Likelihood-Funktion
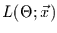 , die angibt, welcher
Wert des gesuchten Parameters
, die angibt, welcher
Wert des gesuchten Parameters 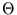 bei der vorgegebenen Stichprobe
bei der vorgegebenen Stichprobe
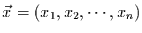 wie wahrscheinlich ist. Das Maximum
dieser Funktion in Abhängigkeit von
wie wahrscheinlich ist. Das Maximum
dieser Funktion in Abhängigkeit von 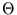 bei gegebener Stichprobe
bei gegebener Stichprobe
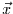 ist der Wert der ML-Schätzung. Um die Likelihood-Funktion zu
erzeugen, entscheidet man sich aufgrund seiner Erfahrung (oder ähnlich
überzeugender Argumente) dafür, daß die Stichprobe aus einem bestimmten
Modell stammt. Das Modell kann dann Stichproben erzeugen. Die
Likelihood-Funktion ist nun die Wahrscheinlichkeit für eine Realisation
ist der Wert der ML-Schätzung. Um die Likelihood-Funktion zu
erzeugen, entscheidet man sich aufgrund seiner Erfahrung (oder ähnlich
überzeugender Argumente) dafür, daß die Stichprobe aus einem bestimmten
Modell stammt. Das Modell kann dann Stichproben erzeugen. Die
Likelihood-Funktion ist nun die Wahrscheinlichkeit für eine Realisation
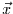 in Abhängigkeit von den
in Abhängigkeit von den 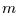 Parametern
Parametern
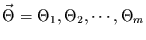 des angenommenen Modells. Die
Likelihood-Funktion braucht dann nur noch uminterpretiert zu werden. Man
betrachtet nicht die Wahrscheinlichkeit für die
des angenommenen Modells. Die
Likelihood-Funktion braucht dann nur noch uminterpretiert zu werden. Man
betrachtet nicht die Wahrscheinlichkeit für die 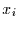 in Abhängigkeit von
in Abhängigkeit von
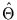 , sondern
, sondern 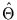 als Variablen und die
als Variablen und die 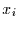 als
Parameter.
Ein Beispiel soll das verdeutlichen. Als Modell für die Stichprobe
wird angenommen, sie stamme aus Gauß'schem weißen Rauschen. Dann ist jeder
einzelne Wert von
als
Parameter.
Ein Beispiel soll das verdeutlichen. Als Modell für die Stichprobe
wird angenommen, sie stamme aus Gauß'schem weißen Rauschen. Dann ist jeder
einzelne Wert von 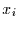 unabhängig von den anderen Werten von
unabhängig von den anderen Werten von 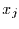 . Alle
Werte sind Gauß-verteilt und stammen somit aus einer Verteilung mit den zwei
Parametern
. Alle
Werte sind Gauß-verteilt und stammen somit aus einer Verteilung mit den zwei
Parametern 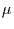 und
und 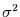 . Wegen (und nur wegen) der Unabhängigkeit
der Einzelereignisse kann die Likelihood-Funktion faktorisiert werden:
. Wegen (und nur wegen) der Unabhängigkeit
der Einzelereignisse kann die Likelihood-Funktion faktorisiert werden:
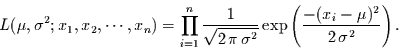 |
(1) |
Daraus folgt
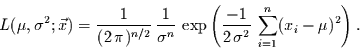 |
(2) |
Man könnte diese Funktion nun nach 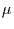 und nach
und nach 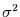 ableiten, die
Ableitungen jeweils nullsetzen und damit die beiden Parameter bestimmen. Dies
wäre recht aufwendig. Und da das nicht das einzige Beispiel ist, bei dem das
recht aufwendig ist, geht man prinzipiell etwas anders vor. Man logarithmiert
die Likelihood-Funktion vor dem ableiten und kommt somit zur
Loglikelihood-Funktion
ableiten, die
Ableitungen jeweils nullsetzen und damit die beiden Parameter bestimmen. Dies
wäre recht aufwendig. Und da das nicht das einzige Beispiel ist, bei dem das
recht aufwendig ist, geht man prinzipiell etwas anders vor. Man logarithmiert
die Likelihood-Funktion vor dem ableiten und kommt somit zur
Loglikelihood-Funktion 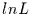 :
:
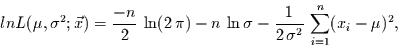 |
(3) |
mit den partiellen Ableitungen
Die Lösung dieses Gleichungssystems ist überraschenderweise der
Momentenschätzer.
Maximum-Likelihood-Schätzer sind
- konsistent
- zumindest asymptotisch erwartungstreu
- zumindest asymptotisch wirksamst
- suffizient
- bester asymptotisch normaler Schätzer.
Gerade die letzte Eigenschaft ist von besonderer Bedeutung. Sie erlaubt es
nämlich nicht nur den wahrscheinlichsten Wert für den Schätzer anzugeben,
sondern auch dessen Verteilung (zumindest asymptotisch). Kennt man aber die
Verteilung des Schätzers, so kann man auch Gleichungen für andere Parameter
als den Erwartunsgwert herleiten. So kann z.B. die Varianz des Erwartungswertes
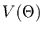 geschätzt werden. Damit lassen sich Konfidenzintervalle angeben,
in denen der geschätzte Parameter mit einer vorgegebenen Wahrscheinlichkeit
liegt.
Abschließend sei noch bemerkt, daß die Likelihood-Funktion keine
Wahrscheinlichkeitsdichte ist. Das ist sie nur, wenn sie normiert wird. Dann
müßte man meines Erachtens aus dieser Likelihood-Funktion die gleiche
Information entnehmen können, wie aus einer Bayes'schen Vorgehensweise.
geschätzt werden. Damit lassen sich Konfidenzintervalle angeben,
in denen der geschätzte Parameter mit einer vorgegebenen Wahrscheinlichkeit
liegt.
Abschließend sei noch bemerkt, daß die Likelihood-Funktion keine
Wahrscheinlichkeitsdichte ist. Das ist sie nur, wenn sie normiert wird. Dann
müßte man meines Erachtens aus dieser Likelihood-Funktion die gleiche
Information entnehmen können, wie aus einer Bayes'schen Vorgehensweise.


Nächste Seite: Bayes-Schätzer
Aufwärts: Schätzverfahren
Vorherige Seite: Methode der kleinsten Quadrate
ich
2000-01-24