

Nächste Seite: Maximum-Likelihood-Schätzer
Aufwärts: Schätzverfahren
Vorherige Seite: Momentenverfahren
Diese auf Gauß und Laplace zurückgehende Methode sieht die Stichprobe als
Summe einer Funktion
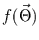 des Parametervektors
des Parametervektors 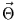 plus
Rauschen an. Dabei muß der Stichprobenumfang größer sein, als die
Dimension des Parametervektors.
plus
Rauschen an. Dabei muß der Stichprobenumfang größer sein, als die
Dimension des Parametervektors. 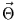 wird nun aus der Stichprobe
so geschätzt, das das Rauschen minimiert wird. Dazu wird zunächst die Summe
der Abstandsquadrate
wird nun aus der Stichprobe
so geschätzt, das das Rauschen minimiert wird. Dazu wird zunächst die Summe
der Abstandsquadrate
![$S=\sum\limits_{i=1}^{n}\left[y_{i}-f\left(\hat{\vec{\Theta}}\right)\right]^{2}$](img23.gif) gebildet und dann minimiert, indem man dessen Ableitung nach dem
Schätzparametervektor
gebildet und dann minimiert, indem man dessen Ableitung nach dem
Schätzparametervektor
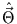 null setzt. Daraus folgt
null setzt. Daraus folgt
![$\sum\limits_{i=1}^{n}\left[y_{i}-f\left(\hat{\vec{\Theta}}\right)\right]
\frac{\partial \hat{\vec{\Theta}}}{\partial \hat{\Theta}_{i}}=0 $](img25.gif) für alle
für alle
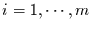 , wenn der Parametervektor
, wenn der Parametervektor 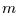 -dimensional ist.
-dimensional ist.
ich
2000-01-24
![$S=\sum\limits_{i=1}^{n}\left[y_{i}-f\left(\hat{\vec{\Theta}}\right)\right]^{2}$](img23.gif) gebildet und dann minimiert, indem man dessen Ableitung nach dem
Schätzparametervektor
gebildet und dann minimiert, indem man dessen Ableitung nach dem
Schätzparametervektor