


Nächste Seite: Anderson-Darling-Test
Aufwärts: Test auf White-Noise
Vorherige Seite: Test auf White-Noise
Inhalt
Untersucht wird die größte vorkommende Abweichung 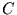 von der Diagonalen:
von der Diagonalen:
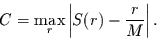 |
(2.10) |
Für 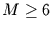 und
und
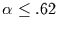 gilt in guter Näherung:
gilt in guter Näherung:
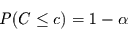 |
(2.11) |
mit
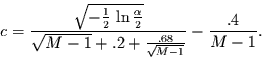 |
(2.12) |
Invertiert man die Abhängigkeit 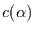 zu
zu 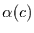 , so gibt
, so gibt
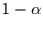 an, wie unwahrscheinlich es ist, daß ein White-Noise-Prozeß
vorliegt und trotzdem ein so hoher Wert von c. Also geht man wie folgt vor:
Man berechnet
an, wie unwahrscheinlich es ist, daß ein White-Noise-Prozeß
vorliegt und trotzdem ein so hoher Wert von c. Also geht man wie folgt vor:
Man berechnet 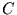 , setzt
, setzt 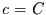 und berechnet die Unwahrscheinlichkeit
und berechnet die Unwahrscheinlichkeit
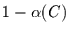 mit der ein solcher Wert bei einem White-Noise-Prozeß
auftritt. Die Inversion von Gleichung (2.12) führt zur
Ablehnungswahrscheinlichkeit der Nullhypothese
mit der ein solcher Wert bei einem White-Noise-Prozeß
auftritt. Die Inversion von Gleichung (2.12) führt zur
Ablehnungswahrscheinlichkeit der Nullhypothese 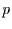 :
:
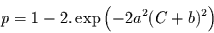 |
(2.13) |
mit
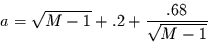 |
(2.14) |
und
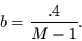 |
(2.15) |
Schlittgen und Streitberg (1994, S. 376) haben gezeigt, daß dieser Test
schlecht ist im Vergleich zum



Nächste Seite: Anderson-Darling-Test
Aufwärts: Test auf White-Noise
Vorherige Seite: Test auf White-Noise
Inhalt
ich
2000-01-25