

Nächste Seite: Der Einfluß der Verwendung
Aufwärts: Berechnung der spektralen Dichte
Vorherige Seite: Berechnung der spektralen Dichte
Inhalt
Betrachtet man die letzte Spalte von Tabelle 1.1 genauer, so sieht man,
daß bei den Frequenzen
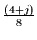 das konjugiert Komplexe zu den
Werten bei
den Frequenzen
das konjugiert Komplexe zu den
Werten bei
den Frequenzen
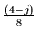 steht. Dies ist kein Zufall. Da die
Beispielzeitreihe aus 8 Werten besteht, kann die Fourier-Darstellung nicht aus
mehr Werten bestehen (da die Fourier-Frequenzen orthogonal sind; hätte jede
der 8 Fourier-Komponenten Real- und Imaginärteil, und wären diese
unabhängig, ergäbe das 16 Informationen).
Man kann nun schließen, daß für Fourier-Frequenzen, die größer sind als
steht. Dies ist kein Zufall. Da die
Beispielzeitreihe aus 8 Werten besteht, kann die Fourier-Darstellung nicht aus
mehr Werten bestehen (da die Fourier-Frequenzen orthogonal sind; hätte jede
der 8 Fourier-Komponenten Real- und Imaginärteil, und wären diese
unabhängig, ergäbe das 16 Informationen).
Man kann nun schließen, daß für Fourier-Frequenzen, die größer sind als
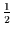 , keine neue Information ins Spiel kommt. Wie kommt das?
Um eine Schwingung abzutasten benötigt man mindestens
zwei Meßpunkte pro Periode.
Hat man in seiner Zeitreihe nun Schwingungen, die hochfrequenter
sind als eine
Schwingung pro
zwei Meßpunkte, d.h. (
, keine neue Information ins Spiel kommt. Wie kommt das?
Um eine Schwingung abzutasten benötigt man mindestens
zwei Meßpunkte pro Periode.
Hat man in seiner Zeitreihe nun Schwingungen, die hochfrequenter
sind als eine
Schwingung pro
zwei Meßpunkte, d.h. (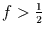 ) so wird diese Schwingung zwar
registriert, aber deren Frequenz wird mißgedeutet.
Diese Frequenzmißdeutung heißt
Aliasing.
Die Frequenz, die die noch aufgelösten von den unaufgelösten Schwingungen
trennt, heißt Nyquist-Frequenz
) so wird diese Schwingung zwar
registriert, aber deren Frequenz wird mißgedeutet.
Diese Frequenzmißdeutung heißt
Aliasing.
Die Frequenz, die die noch aufgelösten von den unaufgelösten Schwingungen
trennt, heißt Nyquist-Frequenz
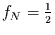 . Nun kann die
Fourier-Zerlegung nicht zwischen Schwingungen der Frequenz
. Nun kann die
Fourier-Zerlegung nicht zwischen Schwingungen der Frequenz
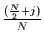 und
und
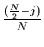 unterscheiden.
Deshalb erhalten beide Frequenzen den gleichen Betrag, sind aber konjugiert
komplex. Es ist zu beachten, daß dieses Aliasing nur für Perioden
zwischen
unterscheiden.
Deshalb erhalten beide Frequenzen den gleichen Betrag, sind aber konjugiert
komplex. Es ist zu beachten, daß dieses Aliasing nur für Perioden
zwischen 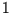 und
und 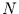 gilt, denn nur solche werden überhaupt von der
Fourier-Zerlegung erfaßt. Was mit Schwingungen bei Perioden kleiner
gilt, denn nur solche werden überhaupt von der
Fourier-Zerlegung erfaßt. Was mit Schwingungen bei Perioden kleiner 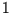 passiert, wird weiter unten besprochen. Zunächst stellt sich die Frage,
welche Schwingung durch die Fourieranalyse auf welche gefaltet wird. Es
werden Schwingungen mit Wellenzahlen zwischen
passiert, wird weiter unten besprochen. Zunächst stellt sich die Frage,
welche Schwingung durch die Fourieranalyse auf welche gefaltet wird. Es
werden Schwingungen mit Wellenzahlen zwischen 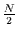 und
und 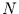 auf
Wellenzahlen kleiner
auf
Wellenzahlen kleiner 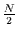 gefaltet. Dadurch wird eine Schwingung
der Wellenzahl
gefaltet. Dadurch wird eine Schwingung
der Wellenzahl 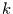 als eine Schwingung der Wellenzahl
als eine Schwingung der Wellenzahl 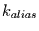 interpretiert.
Es gilt:
interpretiert.
Es gilt:
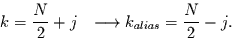 |
(1.7) |
Daraus folgen die Zusammenhänge der Fehlinterpretation:
Das Spektrum, das nur an den Wellenzahlen 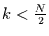 dargestellt wird,
besteht immer aus dem Mittel von dem Frequenzanteil bei der dargestellten und
der dazugehörigen Aliasing-Wellenzahl.
Da dem so ist, scheint es nicht möglich
das Spektrum eindeutig zu interpretieren.
Tatsächlich ist das auch nur möglich, wenn man die Spektralanteile der
Alias-Wellenzahlen unterdrückt (herausfiltert), oder weiß, daß solche
,,hohen`` Frequenzen nicht auftreten.
Die hochfrequenten Anteile (mit
dargestellt wird,
besteht immer aus dem Mittel von dem Frequenzanteil bei der dargestellten und
der dazugehörigen Aliasing-Wellenzahl.
Da dem so ist, scheint es nicht möglich
das Spektrum eindeutig zu interpretieren.
Tatsächlich ist das auch nur möglich, wenn man die Spektralanteile der
Alias-Wellenzahlen unterdrückt (herausfiltert), oder weiß, daß solche
,,hohen`` Frequenzen nicht auftreten.
Die hochfrequenten Anteile (mit 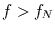 )
kann man nur herausfiltern, wenn man sie auch gemessen hat, d.h. man muß
eine deutlich höhere (z.B. Faktor 10) Abtastrate haben und die so erzeugte
Zeitreihe tiefpaßfiltern. Erst dann kann man ein Aliasing-freies
Periodogramm berechnen. Man weiß dann, daß der spektrale Varianzanteil bei
Schwingungen mit
)
kann man nur herausfiltern, wenn man sie auch gemessen hat, d.h. man muß
eine deutlich höhere (z.B. Faktor 10) Abtastrate haben und die so erzeugte
Zeitreihe tiefpaßfiltern. Erst dann kann man ein Aliasing-freies
Periodogramm berechnen. Man weiß dann, daß der spektrale Varianzanteil bei
Schwingungen mit 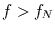 aus der Fourier-Zerlegung stammt,
denn aus der Zeitreihe ist er herausgefiltert. Deshalb muß der durch die
Fourier-Zerlegung in den hohen Spektralbereich gefaltete Anteil wieder
zurückgefaltet werden. Dies geschieht, indem man alle Varianzanteile bei
aus der Fourier-Zerlegung stammt,
denn aus der Zeitreihe ist er herausgefiltert. Deshalb muß der durch die
Fourier-Zerlegung in den hohen Spektralbereich gefaltete Anteil wieder
zurückgefaltet werden. Dies geschieht, indem man alle Varianzanteile bei
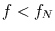 verdoppelt. Man erhält somit das Varianzspektrum der Zeitreihe.
Teilt man dieses durch die Gesamtvarianz, so erhält man die spektrale
Varianzdichte
verdoppelt. Man erhält somit das Varianzspektrum der Zeitreihe.
Teilt man dieses durch die Gesamtvarianz, so erhält man die spektrale
Varianzdichte
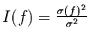 .
Für das Beispiel aus Tabelle 1.1 bedeutet das, daß man wissen muß,
daß Frequenzen mit
.
Für das Beispiel aus Tabelle 1.1 bedeutet das, daß man wissen muß,
daß Frequenzen mit 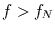 nicht vorkommen. Damit ist vom Spektrum nur der
auswertbare Teil mit
nicht vorkommen. Damit ist vom Spektrum nur der
auswertbare Teil mit
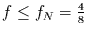 von Interesse. Da die Wellenzahl
von Interesse. Da die Wellenzahl
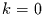 den Mittelwert repräsentiert, bleiben also nur noch die Wellenzahlen
1 bis 4 auswertbar (4 ist in diesem Fall
die Nyquist-Wellenzahl), von denen die spektralen
Varianzen von
den Mittelwert repräsentiert, bleiben also nur noch die Wellenzahlen
1 bis 4 auswertbar (4 ist in diesem Fall
die Nyquist-Wellenzahl), von denen die spektralen
Varianzen von 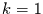 bis
bis 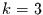 verdoppelt werden (man beachte, das bei
ungeradzahliger Zeitreihenlänge die Nyquistfrequenz nicht auf eine
Stützstelle fällt. Dann muß der zugehörige Wert auch verdoppelt werden).
Damit folgt für die spektralen Varianzanteile aus dem Beispiel:
verdoppelt werden (man beachte, das bei
ungeradzahliger Zeitreihenlänge die Nyquistfrequenz nicht auf eine
Stützstelle fällt. Dann muß der zugehörige Wert auch verdoppelt werden).
Damit folgt für die spektralen Varianzanteile aus dem Beispiel:
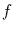 |
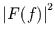 |
Nach Rückfaltung |
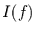 |
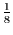 |
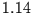 |
2.28 |
.456 |
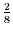 |
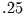 |
.5 |
.1 |
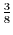 |
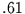 |
1.22 |
.244 |
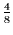 |
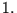 |
1. |
.2 |
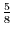 |
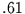 |
|
|
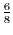 |
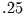 |
|
|
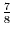 |
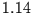 |
|
|
| Summe= |
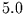 |
5.0 |
1.0 |
Die kleinste durch die Fourier-Zerlegung aufgelöste (wenn auch
mißgedeutete) Periode ist knapp über 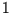 . Was aber ist mit noch hochfrequenteren
Schwingungen, deren Perioden also kleiner als eins sind. Diese können
im Spektrum nicht vorkommen. Auch solche sehr hohen Frequenzen gehen zwar
nicht explizit, aber jedenfalls fehlgedeutet in das Spektrum ein. Ein
Beispiel kann dies verdeutlichen. Eine Schwingung habe eine Periode von
. Was aber ist mit noch hochfrequenteren
Schwingungen, deren Perioden also kleiner als eins sind. Diese können
im Spektrum nicht vorkommen. Auch solche sehr hohen Frequenzen gehen zwar
nicht explizit, aber jedenfalls fehlgedeutet in das Spektrum ein. Ein
Beispiel kann dies verdeutlichen. Eine Schwingung habe eine Periode von
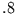 der Abtastrate. Zum Zeitpunkt
der Abtastrate. Zum Zeitpunkt 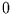 beginne auch die Schwingung. Dann
werden zum Zeitpunkt
beginne auch die Schwingung. Dann
werden zum Zeitpunkt 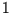 fünf Viertel der Schwingung stattgefunden haben,
was wegen der Abtastung erscheint wie ein Viertel. Zum Zeitpunkt
fünf Viertel der Schwingung stattgefunden haben,
was wegen der Abtastung erscheint wie ein Viertel. Zum Zeitpunkt 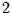 haben
2.5 Schwingungen stattgefunden, was wie eine halbe Schwingung erscheint.
Wie man sich weiter überlegen kann, wird die Schwingung der Periode
haben
2.5 Schwingungen stattgefunden, was wie eine halbe Schwingung erscheint.
Wie man sich weiter überlegen kann, wird die Schwingung der Periode 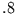 als
Schwingung der Periode
als
Schwingung der Periode 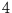 fehlinterpretiert. Dieser Effekt liegt nicht an
der Fourier-Zerlegung, ist also vom oben besprochenen Aliasing zu
unterscheiden. Zumindest für
fehlinterpretiert. Dieser Effekt liegt nicht an
der Fourier-Zerlegung, ist also vom oben besprochenen Aliasing zu
unterscheiden. Zumindest für 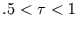 folgt dann der fehlinterpretierte
Wert
folgt dann der fehlinterpretierte
Wert 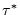 mit
mit
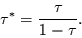 |
(1.8) |
Die einfachste Art dieses Problem zu umgehen, ist die Verwendung von
Mittelwerten, die die hohen Frequenzen herausfiltern. Die beliebten einfachen
Intervallmittel (Jahresmittel, Monatsmittel, Tagesmittel) haben allerdings
nicht den angenehmsten Einfluß auf das Spektrum.



Nächste Seite: Der Einfluß der Verwendung
Aufwärts: Berechnung der spektralen Dichte
Vorherige Seite: Berechnung der spektralen Dichte
Inhalt
ich
2000-01-25