

Nächste Seite: Autokorrelationsspektralanalyse (ASA)
Aufwärts: Berechnung der spektralen Dichte
Vorherige Seite: Aliasing
Inhalt
Im folgenden wird eine spezielle
Art der zeitlichen Mittelung weiter untersucht.
Diese ist zwar nicht
die für Spektralanalysen sinnvollste Art der Mittelung,
aber immerhin die am häufigsten verwendete. Es handelt sich dabei um die
Untersuchung von Zeitreihen von Zeitmitteln. D.h. es wird nicht zu bestimmten
Zeitpunkten ein Meßwert aufgenommen und daraus ergibt sich die Zeitreihe,
sondern es wird immer über konstante Zeiträume gemittelt. Die so
entstehenden Zeitreihen sind dann z.B. Zeitreihen von Jahres-, Monats- oder
Tagesmittelwerten. Um den Einfluß dieser Mittelung zu untersuchen, werden
harmonische Schwingungen der Amplitude 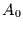 und Phase
und Phase 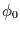 betrachtet:
betrachtet:
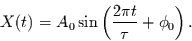 |
(1.9) |
Tastet man diese Funktion in Abständen 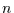 ab, so erhält man die Folge:
ab, so erhält man die Folge:
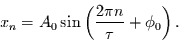 |
(1.10) |
Für die Folge der Mittelwerte über Intervalle der Länge 1 gilt:
Nun ist
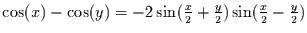 und deshalb folgt:
und deshalb folgt:
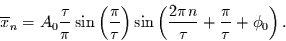 |
(1.11) |
Demnach führt der Filter (Verwendung von Mittelwertzeitreihen) zur
Amplitudendämpfung 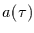 und Phasendrehung
und Phasendrehung 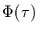 mit:
mit:
Man beachte, daß für große Perioden 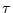 die Phasenverschiebung
gegen null und die Amplitudendämpfung gegen eins geht, das heißt
niederfrequente Schwingungen werden von dem Filter nicht verändert.
Für kleine Werte von
die Phasenverschiebung
gegen null und die Amplitudendämpfung gegen eins geht, das heißt
niederfrequente Schwingungen werden von dem Filter nicht verändert.
Für kleine Werte von 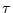 wird
wird
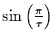 immer schneller alternieren. Andererseits wird
immer schneller alternieren. Andererseits wird
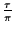 immer
kleiner werden. Daraus folgt, daß
immer
kleiner werden. Daraus folgt, daß 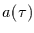 für kleine
für kleine 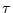 alternierend
gegen null konvergiert. Wie man sich leicht klar machen kann, werden die
Schwingungen mit
alternierend
gegen null konvergiert. Wie man sich leicht klar machen kann, werden die
Schwingungen mit
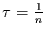 exakt weggefiltert. Für
dazwischenliegende Werte von
exakt weggefiltert. Für
dazwischenliegende Werte von 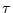 sind die Amplituden durch die
Einhüllende der Amplitudendämpfung
sind die Amplituden durch die
Einhüllende der Amplitudendämpfung
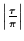 begrenzt.
Nun interessiert nicht die Amplitudendämpfung des Filters, sondern der
dadurch hervorgerufene Einfluß auf das Varianzspektrum. Dieser Einfluß
wird im Folgenden berechnet. Zunächst ist die Varianz gegeben durch:
begrenzt.
Nun interessiert nicht die Amplitudendämpfung des Filters, sondern der
dadurch hervorgerufene Einfluß auf das Varianzspektrum. Dieser Einfluß
wird im Folgenden berechnet. Zunächst ist die Varianz gegeben durch:
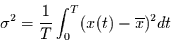 |
(1.14) |
Dabei sei 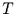 der Beobachtungszeitraum und
der Beobachtungszeitraum und 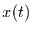 eine harmonische
Schwingung gemäß Glg. (1.9). Unter der Annahme
eine harmonische
Schwingung gemäß Glg. (1.9). Unter der Annahme 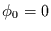 vereinfacht
sich der Ausdruck für die Varianz der harmonischen Schwingung zu:
vereinfacht
sich der Ausdruck für die Varianz der harmonischen Schwingung zu:
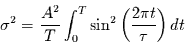 |
(1.15) |
mit der Lösung
Die Ungleichung gilt, da nur Perioden kleiner als der Meßzeitraum aufgelöst
werden. Mit
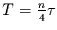 (und
(und 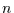 aus den natürlichen Zahlen) folgt exakt
aus den natürlichen Zahlen) folgt exakt
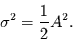 |
(1.16) |
Die Varianz einer konkreten Schwingung hängt erst durch die Einführung des Filters von der Periode
ab. Dann nämlich gilt
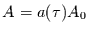 und somit für die spektrale Varianz
der gefilterten Reihe:
und somit für die spektrale Varianz
der gefilterten Reihe:
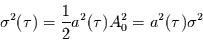 |
(1.17) |
Will man also aus dem berechneten Spektrum der Mittelwertzeitreihe auf das
Spektrum der zugrundeliegenden Zeitreihe schließen, so muß man dieses mit
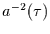 multiplizieren. Dabei gilt für
multiplizieren. Dabei gilt für 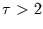 (d.h. Frequenzen
kleiner als die Nyquist-Frequenz) in guter Näherung (Fehler kleiner
.5 %) die abgebrochene Reihenentwicklung:
(d.h. Frequenzen
kleiner als die Nyquist-Frequenz) in guter Näherung (Fehler kleiner
.5 %) die abgebrochene Reihenentwicklung:
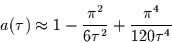 |
(1.18) |
Der Einfluß des Filters auf das Spektrum ist in Abbildung 1.1
dargestellt. In Tabelle 1.2 sind einige Zahlenwerte zusammengefaßt.
Wie man sieht, ist der Filter keineswegs optimal, denn
- weder werden
Schwingungen mit Perioden größer
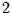 nicht beeinflußt,
nicht beeinflußt,
- noch werden
Schwingungen mit Perioden kleiner
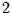 vollständig weggedämpft.
vollständig weggedämpft.
Gerade
zwischen 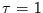 und
und 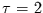 bleibt noch bis zu
bleibt noch bis zu 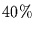 der Varianz der
Schwingung erhalten und wird durch Aliasing in das Spektrum hineingefaltet.
Es kann dann nicht mehr von dem dortigen Spektralanteil unterschieden werden.
Schwingungen mit Perioden kleiner
der Varianz der
Schwingung erhalten und wird durch Aliasing in das Spektrum hineingefaltet.
Es kann dann nicht mehr von dem dortigen Spektralanteil unterschieden werden.
Schwingungen mit Perioden kleiner 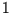 werden fast vollständig weggefiltert,
so daß höchstens
werden fast vollständig weggefiltert,
so daß höchstens 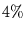 von ihnen übrigbleiben und in das Spektrum
einfließen.
von ihnen übrigbleiben und in das Spektrum
einfließen.
Abbildung:
Vom Periodogramm erkannter Anteil der Varianz bei
verschiedenen Perioden. Für 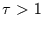 ist die Reihennäherung gepunktet
eingezeichnet.
ist die Reihennäherung gepunktet
eingezeichnet.
|
hb
Tabelle 1.2:
Wirkung der Verwendung von Mittelwerten.
 |
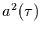 |
| .66 |
.0450 |
| 1 |
.0000 |
| 2 |
.4015 |
| 3 |
.6839 |
| 4 |
.8105 |
| 5 |
.8752 |
| 6 |
.9118 |
| 7 |
.9347 |
| 8 |
.9497 |
| 9 |
.9600 |
| 10 |
.9675 |
| 15 |
.9855 |



Nächste Seite: Autokorrelationsspektralanalyse (ASA)
Aufwärts: Berechnung der spektralen Dichte
Vorherige Seite: Aliasing
Inhalt
ich
2000-01-25
![\begin{eqnarray*}
\overline{x}_{n} & = & \int_{n}^{n+1} A_{0}\sin\left(\frac{2\...
...)
-\cos\left(\frac{2\pi (n+1)}{\tau}+\phi_{0}\right)\right].
\end{eqnarray*}](img81.gif)