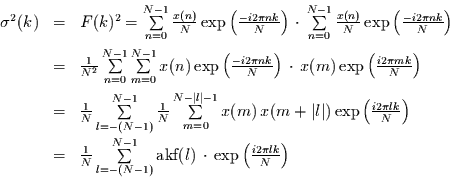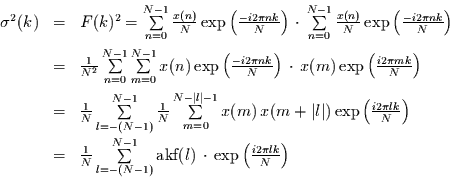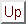


Nächste Seite: Ein Beispiel zum Vergleich
Aufwärts: Spektrale Dichte
Vorherige Seite: Der Einfluß der Verwendung
Inhalt
Nach dem Wiener-Chinchin-Theorem kann das Spektrum auch aus der
Autokorrelationsfunktion geschätzt werden. Dies ist leicht zu sehen, denn
nach Glg. (1.3) gilt für die spektrale Dichte
Dabei ist akf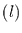 die Autokorrelationsfunktion zur Verschiebung
die Autokorrelationsfunktion zur Verschiebung 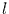 .
Die spektrale Dichte ist demnach auch die Fourier-Transformierte der
Autokorrelationsfunktion. Berechnet man sie auf diesem Weg, so bezeichnet man
dies als Autokorrelationsspektralanalyse (ASA).
Benutzt man die ASA zur Schätzung des Spektrums, so stellt sich
die Frage, bis zu welcher Verschiebung man die Autokorrelationsfunktion
verwendet.
Als ersten Schritt, könnte man einen bestimmten Wert vorgeben (z.B. ein
Viertel der Zeitreihenlänge). Je kleiner dieser Wert ist, desto glatter
wird das Spektrum. Das bedeutet einerseits, daß unzverlässige Peaks
vermieden werden, andererseits, daß auch die zuverlässigen Peaks zumindest
teilweise unterdrückt werden könnten. Benachbarte Peaks können durch
die Wahl von zu wenig berücksichtigten Zeitverschiebungen zu einem einzigen
Peak zusammenschmelzen. Dies kann erhebliche Mißdeutungen zur Folge habe.
Eine durchaus bessere Methode ist es, alle diejenigen
Autokorrelationsfunktionswerte zu verwenden, die sich signifikant (auf einem
vorzugebenden Niveau) von null unterschieden und alle nicht signifikanten
Autokorrelationswerte auf null zu setzen. Eine weitere Möglichkeit ist
es, den Autokorrelationskoeffizienten bei größeren Verschiebungen immer
weniger Gewicht zu geben. Dies geschieht z.B. durch das Hamming Window:
.
Die spektrale Dichte ist demnach auch die Fourier-Transformierte der
Autokorrelationsfunktion. Berechnet man sie auf diesem Weg, so bezeichnet man
dies als Autokorrelationsspektralanalyse (ASA).
Benutzt man die ASA zur Schätzung des Spektrums, so stellt sich
die Frage, bis zu welcher Verschiebung man die Autokorrelationsfunktion
verwendet.
Als ersten Schritt, könnte man einen bestimmten Wert vorgeben (z.B. ein
Viertel der Zeitreihenlänge). Je kleiner dieser Wert ist, desto glatter
wird das Spektrum. Das bedeutet einerseits, daß unzverlässige Peaks
vermieden werden, andererseits, daß auch die zuverlässigen Peaks zumindest
teilweise unterdrückt werden könnten. Benachbarte Peaks können durch
die Wahl von zu wenig berücksichtigten Zeitverschiebungen zu einem einzigen
Peak zusammenschmelzen. Dies kann erhebliche Mißdeutungen zur Folge habe.
Eine durchaus bessere Methode ist es, alle diejenigen
Autokorrelationsfunktionswerte zu verwenden, die sich signifikant (auf einem
vorzugebenden Niveau) von null unterschieden und alle nicht signifikanten
Autokorrelationswerte auf null zu setzen. Eine weitere Möglichkeit ist
es, den Autokorrelationskoeffizienten bei größeren Verschiebungen immer
weniger Gewicht zu geben. Dies geschieht z.B. durch das Hamming Window:
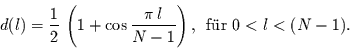 |
(1.19) |
Dann folgt für den Schätzer des Spektrums:
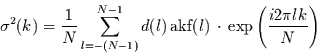 |
(1.20) |



Nächste Seite: Ein Beispiel zum Vergleich
Aufwärts: Spektrale Dichte
Vorherige Seite: Der Einfluß der Verwendung
Inhalt
ich
2000-01-25