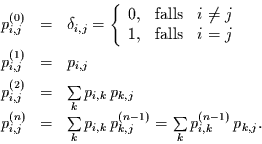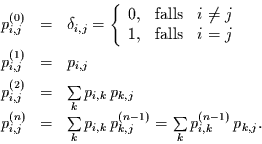


Nächste Seite: Beispiele
Aufwärts: Markovketten
Vorherige Seite: Markovketten
Inhalt
Markov-Ketten heißen zeitlich homogen (oft einfach homogen genannt),
wenn die Übergangswahrscheinlichkeiten nicht
von der Zeit 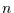 abhängen. Dann hängt auch die Übergangsmatrix nicht von
der Zeit ab. Die Elemente
abhängen. Dann hängt auch die Übergangsmatrix nicht von
der Zeit ab. Die Elemente 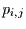 sind dann konstant. Mit
sind dann konstant. Mit 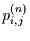 wird nun die Wahrscheinlichkeit bezeichnet, in
wird nun die Wahrscheinlichkeit bezeichnet, in 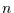 Schritten vom Zustand
Schritten vom Zustand 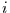 in den Zustand
in den Zustand 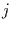 zu gelangen. Dann gilt:
zu gelangen. Dann gilt:
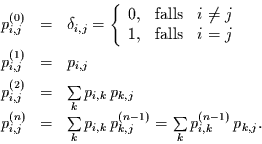 |
(3.6) |
Benutzt man wieder die Matrixschreibweise, so kann man 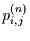 leicht
berechnen, denn die
leicht
berechnen, denn die 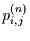 sind die Elemente der
sind die Elemente der 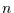 -ten Potenz der
Austauschmatrix. Es gilt also allgemein für die
-ten Potenz der
Austauschmatrix. Es gilt also allgemein für die 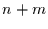 -stufige
Übergangsmatrix
-stufige
Übergangsmatrix
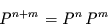 |
(3.7) |
und daher auch für die Elemente
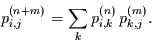 |
(3.8) |
Dies ist die Chapman-Kolmogoroff-Gleichung. Ein Anwendungsbeispiel soll deren
Nutzen verdeutlichen.
Ein System befinde sich zur Zeit 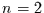 im Zustand
im Zustand 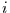 . Wie hoch ist dann die
Wahrscheinlichkeit dafür, daß es sich zur Zeit
. Wie hoch ist dann die
Wahrscheinlichkeit dafür, daß es sich zur Zeit 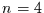 im Zustand
im Zustand 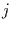 , zur
Zeit
, zur
Zeit 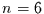 im Zustand
im Zustand 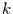 und zur Zeit
und zur Zeit 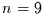 im Zustand
im Zustand 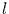 befindet. Es
spielt dabei keine Rolle in welchem Zustand es sich zu den Zeiten
befindet. Es
spielt dabei keine Rolle in welchem Zustand es sich zu den Zeiten
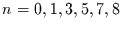 befindet. Die gesuchte Wahrscheinlichkeit folgt direkt aus der
allgemeinen Chapman-Kolmogoroff-Gleichung:
befindet. Die gesuchte Wahrscheinlichkeit folgt direkt aus der
allgemeinen Chapman-Kolmogoroff-Gleichung:



Nächste Seite: Beispiele
Aufwärts: Markovketten
Vorherige Seite: Markovketten
Inhalt
ich
2000-01-24