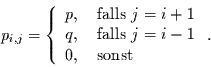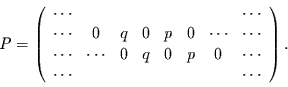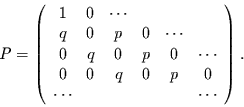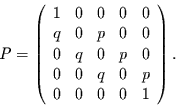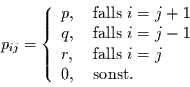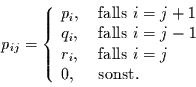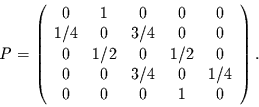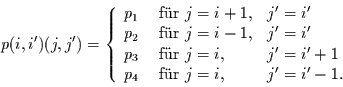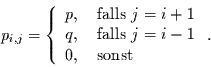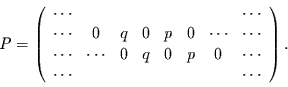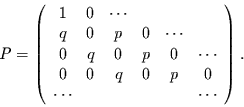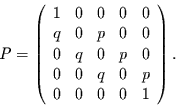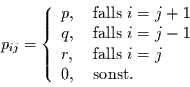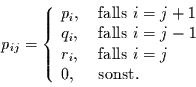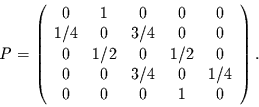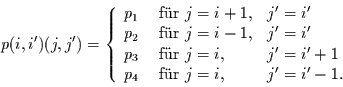


Nächste Seite: Über dieses Dokument ...
Aufwärts: Markovketten
Vorherige Seite: Homogene Markovketten und Chapman-Kolmogoroff-Gleichung
Inhalt
Im folgenden werden einige einfache Beispiele von Markov-Ketten vorgestellt.
- Irrfahrt (Diffusion)
Der Irrfahrer in einem unbegrenzten eindimensionalen Raum ist das
Paradebeispiel für eine Markov-Kette. Der diskrete Wertebereich kann durch
die Menge der ganzen Zahlen ausgedrückt werden. In jedem Zeitschritt wird der
Irrfahrer mit der Wahrscheinlichkeit
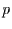 um 1 nach rechts und mit der
Wahrscheinlichkeit
um 1 nach rechts und mit der
Wahrscheinlichkeit 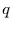 um eins nach links wandern. Eine Trajektorie als
Realisation der Markov-Kette beginnt also bei einer vorgegebenen ganzen Zahl
als Anfangsbedingung und kann mit der Zeit immer weiter von diesem Anfangsort
abdriften. Andererseits kann eine Trajektorie auch sehr lange in der Nähe des
Anfangs bleiben. Falls
um eins nach links wandern. Eine Trajektorie als
Realisation der Markov-Kette beginnt also bei einer vorgegebenen ganzen Zahl
als Anfangsbedingung und kann mit der Zeit immer weiter von diesem Anfangsort
abdriften. Andererseits kann eine Trajektorie auch sehr lange in der Nähe des
Anfangs bleiben. Falls 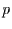 recht groß ist (dann ist
recht groß ist (dann ist 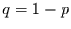 recht klein),
wird der Irrfahrer wahrscheinlicher zu höheren Zahlen abdriften, als zu
niedrigeren. Wie bei jeder Markov-Kette kann man die Wahrscheinlichkeit den
Irrfahrer zu einem bestimmten Zeitpunkt an einem bestimmten Ort zu treffen, mit
Hilfe der Übergangsmatrix und deren Potenzen berechnen. Die Elemente der
Übergangsmatrix folgen aus der Bedingung, daß der Irrfahrer von einem
Zustand
recht klein),
wird der Irrfahrer wahrscheinlicher zu höheren Zahlen abdriften, als zu
niedrigeren. Wie bei jeder Markov-Kette kann man die Wahrscheinlichkeit den
Irrfahrer zu einem bestimmten Zeitpunkt an einem bestimmten Ort zu treffen, mit
Hilfe der Übergangsmatrix und deren Potenzen berechnen. Die Elemente der
Übergangsmatrix folgen aus der Bedingung, daß der Irrfahrer von einem
Zustand 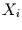 nur in die beiden benachbarten Zustände
nur in die beiden benachbarten Zustände 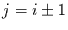 kommen
kann. Damit hat die Übergangsmatrix nur in den Nebendiagonalen von 0
verschiedene Elemente. Es gilt
kommen
kann. Damit hat die Übergangsmatrix nur in den Nebendiagonalen von 0
verschiedene Elemente. Es gilt
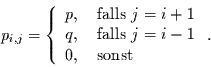 |
(3.9) |
Für die unendlich große Übergangsmatrix folgt dann
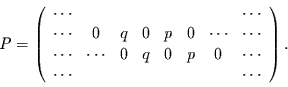 |
(3.10) |
Für praktische Berechnungen benötigt man diese unendlich große Matrix
nicht. Für den ersten Zeitschritt wird zum Beispiel nur ein Ausschnitt mit
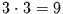 Elementen benötigt. Für
Elementen benötigt. Für 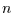 Zeitschritte wird eine Matrix der
Größe
Zeitschritte wird eine Matrix der
Größe 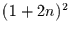 benötigt. Nach
benötigt. Nach 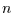 Zeitschritten kann der Irrfahrer
maximal
Zeitschritten kann der Irrfahrer
maximal 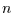 Orte von seiner Startposition entfernt sein. Am Beispiel des
Irrfahrers läßt sich sehr viel veranschaulichen, so daß wir darauf
zurückkommen werden.
Orte von seiner Startposition entfernt sein. Am Beispiel des
Irrfahrers läßt sich sehr viel veranschaulichen, so daß wir darauf
zurückkommen werden.
- Irrfahrt mit einem absorbierenden Rand (Ruinproblem)
In diesem Fall steht dem Irrfahrer kein unbegrenzter Raum in beiden Richtungen
zur Verfügung. Stattdessen soll bei 0 ein Rand sein. Dadurch wird der
Wertebereich auf die Menge der natürlichen Zahlen eingeschränkt. Falls der
Irrfahrer nun bei 0 vorbeikommt wird er dort gefangen werden, d.h.
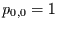 und
und
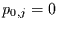 für alle
für alle 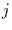 . Da man den Anfangszustand als Kapital zu Beginn
einer
Reihe von aufeinanderfolgenden Einzelspielen mit jeweils gleicher
Gewinnwahrscheinlichkeit ansehen kann, wird diese Form der Irrfahrt in der
Spieltheorie als Ruinproblem bezeichnet. Falls man einmal kein Kapital mehr
besitzt, ist das Spiel verloren. Die Übergangsmatrix ist jetzt nur noch in
einer Richtung unendlich weit ausgedehnt:
. Da man den Anfangszustand als Kapital zu Beginn
einer
Reihe von aufeinanderfolgenden Einzelspielen mit jeweils gleicher
Gewinnwahrscheinlichkeit ansehen kann, wird diese Form der Irrfahrt in der
Spieltheorie als Ruinproblem bezeichnet. Falls man einmal kein Kapital mehr
besitzt, ist das Spiel verloren. Die Übergangsmatrix ist jetzt nur noch in
einer Richtung unendlich weit ausgedehnt:
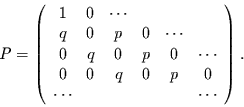 |
(3.11) |
- Irrfahrt mit zwei absorbierenden Rändern
Bei der Irrfahrt mit zwei Rändern ist der Wertebereich endlich. Wir können
den kleinsten Wert 0 und den größten Wert
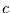 nennen. Dann gilt zusätzlich
zu
nennen. Dann gilt zusätzlich
zu 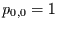 auch noch
auch noch 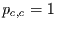 und deshalb auch
und deshalb auch 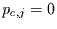 für alle
für alle
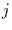 . Wenn die Zustände 0 oder
. Wenn die Zustände 0 oder 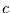 einmal eingenommen sind, ist ein
stationärer
Zustand erreicht. Eine Solche Markov-Kette kann als Nullsummenspiel
zweier Spieler interpretiert werden. Diese machen fortlaufend Spiele
gegeneinander mit gleichbleibender Gewinnwahrscheinlichkeit. Gerecht währe
dabei die Anfangsbedingung, daß jeder
einmal eingenommen sind, ist ein
stationärer
Zustand erreicht. Eine Solche Markov-Kette kann als Nullsummenspiel
zweier Spieler interpretiert werden. Diese machen fortlaufend Spiele
gegeneinander mit gleichbleibender Gewinnwahrscheinlichkeit. Gerecht währe
dabei die Anfangsbedingung, daß jeder 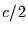 Mark hat. Der Verlierer eines
Spiels zahlt dem Gewinner eine Mark. Die Summe des Geldes ist dabei konstant
(deshalb der Name Nullsummenspiel). Versetzt man sich in die Position des
einen Spielers, so hat er gewonnen, wenn er
Mark hat. Der Verlierer eines
Spiels zahlt dem Gewinner eine Mark. Die Summe des Geldes ist dabei konstant
(deshalb der Name Nullsummenspiel). Versetzt man sich in die Position des
einen Spielers, so hat er gewonnen, wenn er 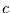 Mark
hat. Er hat verloren, wenn er kein Geld mehr besitzt. Die Wahrscheinlichkeit,
mit der er den Abend gewinnt, hängt von der Anfangsverteilung des Geldes
unter den beiden Spielern und seiner Gewinnwahrscheinlichkeit bei den
Einzelspielen ab. Die Übergangsmatrix, mit der er seine
Gewinnwahrscheinlichkeit berechnen kann ist eine endliche quadratische Matrix
der Ordnung
Mark
hat. Er hat verloren, wenn er kein Geld mehr besitzt. Die Wahrscheinlichkeit,
mit der er den Abend gewinnt, hängt von der Anfangsverteilung des Geldes
unter den beiden Spielern und seiner Gewinnwahrscheinlichkeit bei den
Einzelspielen ab. Die Übergangsmatrix, mit der er seine
Gewinnwahrscheinlichkeit berechnen kann ist eine endliche quadratische Matrix
der Ordnung 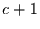 . Für
. Für 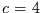 folgt zum Beispiel
folgt zum Beispiel
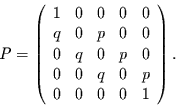 |
(3.12) |
- Irrfahrt mit zwei reflektierenden Rändern
Die Irrfahrt mit reflektierenden Rändern ist als Diffusion in einem
begrenzten Gebiet interpretierbar. Spieltheoretisch ist dieser Fall nicht
besonders interessant, da immer wenn ein Spieler verlieren würde, dieser
wieder ins Spiel gebracht wird. Die Randbedingungen reflektierender Ränder
bei 0 und
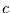 sind gegeben durch
sind gegeben durch 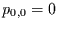 ,
, 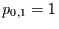 ,
, 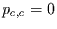 und
und
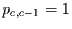 . Bei einer Kette mit den
. Bei einer Kette mit den 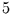 Zuständen 0 bis
Zuständen 0 bis 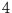 folgt dann
für die Übergangsmatrix
folgt dann
für die Übergangsmatrix
 |
(3.13) |
- Irrfahrt mit Pausen (Unentschiedene Einzelspiele)
Falls der Irrfahrer nicht in jedem Zeitschritt um eine Einheit wandern muß,
sondern mit einer gewissen Wahrscheinlichkeit
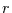 in dem Zustand bleibt, in
dem er gerade ist, so sind auch die Hauptdiagonalen der Übergangsmatrix
gefüllt. Für die Übergangswahrscheinlichkeiten
in dem Zustand bleibt, in
dem er gerade ist, so sind auch die Hauptdiagonalen der Übergangsmatrix
gefüllt. Für die Übergangswahrscheinlichkeiten 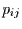 folgt dann
folgt dann
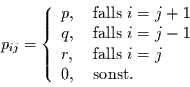 |
(3.14) |
Auch hier ist die Übergangsmatrix von der Ordnung unendlich.
- Nichtlokale Markov-Ketten
Alle bis jetzt explizit besprochenen Markov-Ketten waren lokale Markov-Ketten,
da in jedem Zeitschritt nur direkt benachbarte Zustände erreicht werden
konnten. Dies ist keinesfalls eine notwendige Eigenschaft. Die Formulierung
durch Übergangsmatrizen entfaltet ihren Sinn erst dann klar, wenn nicht nur
die Diagonalen und ersten Nebendiagonalen mit Elementen ungleich 0 gefüllt
sind. Dann sind nicht nur Übergänge zu direkten Nachbarn möglich, und man
spricht von nichtlokalen Ketten.
- Räumlich und zeitlich homogene Markov-Ketten
Die bisher betrachteten Beispiele waren alle zeitlich homogen und räumlich
homogen, da
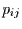 nicht explizit von
nicht explizit von 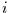 oder
oder 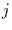 , sondern nur von der
Differenz
, sondern nur von der
Differenz 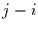 abhingen. Allgemein gilt für räumich homogene Markov-Ketten
abhingen. Allgemein gilt für räumich homogene Markov-Ketten
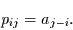 |
(3.15) |
Die Übergangswahrscheinlichkeit ist demnach für jeden Abstand eine
Konstante. Mit 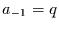 ,
, 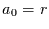 und
und 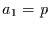 erhält man die Irrfahrt
mit Pausen.
erhält man die Irrfahrt
mit Pausen.
- Zustandsabhängige Markovketten
Zustandsabhängige Markov-Ketten sind räumich nicht homogene Markov-Ketten.
Das bedeutet, das bei diesen Markov-Ketten die Übergangswahrscheinlichkeiten
explizit vom Zustand des Systems abhängen. Es gilt dann z.B. für den
zustandsabhängigen Irrfahrer mit Pausen
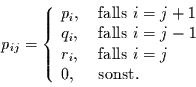 |
(3.16) |
- Ehrenfest-Modell
Das Ehrenfest-Modell ist ein Spezialfall der zustandsabhängigen
Markov-Ketten. Es hat als Wertebereich die Werte
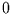 bis
bis 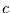 . Die
Übergangswahrscheinlichkeiten hängen nun vom Ort ab, und zwar in der Form
. Die
Übergangswahrscheinlichkeiten hängen nun vom Ort ab, und zwar in der Form
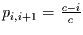 und
und
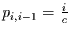 . Das bedeutet, das sich
eine Realisation eher von den Rändern entfernt, als diesen nahe zu
kommen. Für
. Das bedeutet, das sich
eine Realisation eher von den Rändern entfernt, als diesen nahe zu
kommen. Für 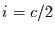 befindet sich die Realisation in der Mitte des
Wertebereichs. Die Übergangswahrscheinlichkeiten für beide Richtungen sind
dann gleich groß. Für ein Ehrenfest-Modell mit den 5 Zuständen 0 bis 4
folgt dann die Übergangsmatrix
befindet sich die Realisation in der Mitte des
Wertebereichs. Die Übergangswahrscheinlichkeiten für beide Richtungen sind
dann gleich groß. Für ein Ehrenfest-Modell mit den 5 Zuständen 0 bis 4
folgt dann die Übergangsmatrix
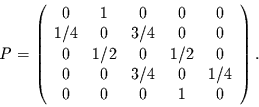 |
(3.17) |
- Wartezeit-Modell
Da Wartezeiten nicht kleiner als 0 sein sollten, ist der Wertebereich des
Wartezeit-Modells durch die natürlichen Zahlen inkl. 0 gegeben. Es werden nun
die Wahrscheinlichkeiten von einem Ort
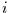 auf
auf 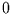 zu springen oder einen Wert
höher (also auf
zu springen oder einen Wert
höher (also auf 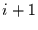 ) zu springen vorgegeben:
) zu springen vorgegeben:
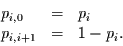 |
(3.18) |
Das bedeutet, daß die Realisation der Markov-Kette entweder um einen Wert
höher springt, oder auf 0 zurückgeht. Der Sprung auf 0 soll nun immer ein
Ereignis darstellen. Dann ist der Wert 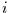 die Zeit, die seit dem letzten
Eintreten des Ereignisses vergangen ist. In einem solchen Wartezeit-Modell ist
es möglich, die Wahrscheinlichkeit für das Eintreten des Ereignisses
beliebig von der Zeit seit dem letzten Eintreten abhängig zu
machen. Betrachtet man den Spezialfall, daß die Wahrscheinlichkeit für das
Eintreten des Ereignisses eine Konstante ist
die Zeit, die seit dem letzten
Eintreten des Ereignisses vergangen ist. In einem solchen Wartezeit-Modell ist
es möglich, die Wahrscheinlichkeit für das Eintreten des Ereignisses
beliebig von der Zeit seit dem letzten Eintreten abhängig zu
machen. Betrachtet man den Spezialfall, daß die Wahrscheinlichkeit für das
Eintreten des Ereignisses eine Konstante ist 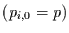 , so ist die
Wahrscheinlichkeit dafür, daß erst im
, so ist die
Wahrscheinlichkeit dafür, daß erst im 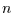 -ten Schritt auf 0 gesprungen wird,
gegeben durch
-ten Schritt auf 0 gesprungen wird,
gegeben durch
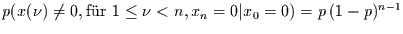 . Das sollte dem interessierten Leser bekannt vorkommen.
. Das sollte dem interessierten Leser bekannt vorkommen.
- Zweidimensionale Irrfahrt
Markov-Ketten können natürlich auch mehrdimensional sein. Das einfachste
Beispiel einer mehrdimensionalen Markov-Kette ist der zweidimensionale
Irrfahrer. Man kann ihn als Zufallswanderer in den Straßen einer sehr
symmetrischen Stadt interpretieren. An jeder Kreuzung hat er vier
Möglichkeiten, von denen jede mit einer bestimmten Wahrscheinlichkeit
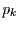 gewählt wird. Wenn der Wanderer keine Pausen machen darf, muß gelten
gewählt wird. Wenn der Wanderer keine Pausen machen darf, muß gelten
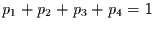 . Die beiden Dimensionen werden nun dadurch formal
unterschieden, daß die zweite Dimension
durch gestrichene Größen dargestellt wird. Damit geht der Zufallswanderer in
jedem Zeitschritt vom Zustand
. Die beiden Dimensionen werden nun dadurch formal
unterschieden, daß die zweite Dimension
durch gestrichene Größen dargestellt wird. Damit geht der Zufallswanderer in
jedem Zeitschritt vom Zustand 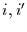 in den Zustand
in den Zustand 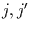 über. Der
Zufallswanderer wird aber immer nur in eine Richtung pro Zeitschritt wandern
können. Es ergibt sich deshalb für die zweidimensionale
Übergangswahrscheinlichkeit
über. Der
Zufallswanderer wird aber immer nur in eine Richtung pro Zeitschritt wandern
können. Es ergibt sich deshalb für die zweidimensionale
Übergangswahrscheinlichkeit
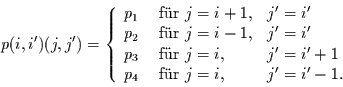 |
(3.19) |



Nächste Seite: Über dieses Dokument ...
Aufwärts: Markovketten
Vorherige Seite: Homogene Markovketten und Chapman-Kolmogoroff-Gleichung
Inhalt
ich
2000-01-24