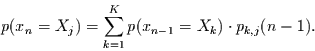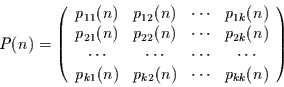


Nächste Seite: Homogene Markovketten und Chapman-Kolmogoroff-Gleichung
Aufwärts: Symbolische Dynamik, Punktprozesse und
Vorherige Seite: Betrachtung bei diskreten Zeitschritten
Inhalt
Markov-Ketten sind wertdiskrete Zufallsprozesse, die entweder
zeitkontinuierlich oder zeitdiskret sein können. Der Einfachheit halber und
weil sie für die Anwendung auf Zeitreihen völlig ausreichend sind, werden
hier nur zeitdiskrete Markov-Ketten besprochen. Die wesentliche Eigenschaft
von Markov-Ketten heißt Markov-Eigenschaft und liegt darin, daß eine
Markov-Kette ihre Vergangenheit vergißt. Man kann Markov-Ketten
verschiedener Ordnung definieren, je nachdem wie weit das Gedächtnis des
Prozesses in die Vergangenheit reichen soll. Umfaßt der Wertebereich des
Prozesses die Werte
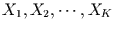 , so kann man fragen, mit
welcher Wahrscheinlichkeit die Zufallsvariable
, so kann man fragen, mit
welcher Wahrscheinlichkeit die Zufallsvariable 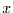 , die die Realisation des
Prozesses darstellt, zum Zeitschritt
, die die Realisation des
Prozesses darstellt, zum Zeitschritt 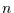 den Wert
den Wert 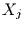 annimmt, wenn zu
vorhergehenden Zeiten bestimmte andere Zustände angenommen wurden. Allgemein
kann diese bedingte Wahrscheinlichkeit
annimmt, wenn zu
vorhergehenden Zeiten bestimmte andere Zustände angenommen wurden. Allgemein
kann diese bedingte Wahrscheinlichkeit
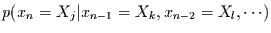 von beliebig vielen vergangenen Realisationen
abhängen. Für eine Markov-Kette
von beliebig vielen vergangenen Realisationen
abhängen. Für eine Markov-Kette 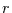 -ter Ordnung hängt die
Wahrscheinlichkeit für eine bestimmte Realisation zur Zeit
-ter Ordnung hängt die
Wahrscheinlichkeit für eine bestimmte Realisation zur Zeit 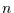 nur von den
vorhergehenden
nur von den
vorhergehenden 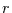 Realisationen ab. Oft wird mit dem Begriff Markov-Kette
nur die Markov-Kette erster Ordnung gemeint, für die die Wahrscheinlichkeit
der Realisation des Wertes
Realisationen ab. Oft wird mit dem Begriff Markov-Kette
nur die Markov-Kette erster Ordnung gemeint, für die die Wahrscheinlichkeit
der Realisation des Wertes 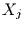 zur Zeit
zur Zeit 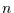 nur von der Wahrscheinlichkeit
der Realisationen aller möglichen Werte
nur von der Wahrscheinlichkeit
der Realisationen aller möglichen Werte 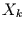 zur Zeit
zur Zeit 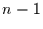 und
zugeordneten Übergangswahrscheinlichkeiten
und
zugeordneten Übergangswahrscheinlichkeiten 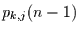 zum Zeitpunkt
zum Zeitpunkt 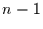 abhängt.
Es gilt dann für die Markov-Kette erster Ordnung
abhängt.
Es gilt dann für die Markov-Kette erster Ordnung
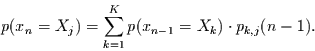 |
(3.1) |
Wenn die Übergangswahrscheinlichkeiten 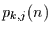 nicht von der Zeit
nicht von der Zeit 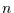 abhängen, spricht man von einer zeitlich homogenen Markov-Kette.
Für die weitere
Untersuchung von Markov-Ketten bietet sich die vereinfachte formelle
Schreibweise
abhängen, spricht man von einer zeitlich homogenen Markov-Kette.
Für die weitere
Untersuchung von Markov-Ketten bietet sich die vereinfachte formelle
Schreibweise
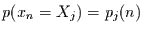 an.
Damit kann Gleichung (3.1) in der handlicheren Form
an.
Damit kann Gleichung (3.1) in der handlicheren Form
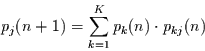 |
(3.2) |
geschrieben werden.
Man kann nun für jeden Zeitpunkt einen Wahrscheinlichkeitsvektor 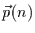 definieren, dessen
definieren, dessen 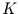 Elemente die Wahrscheinlichkeiten für die Realisation
der
Elemente die Wahrscheinlichkeiten für die Realisation
der 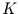 möglichen Zustände sind:
möglichen Zustände sind:
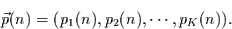 |
(3.3) |
Die Übergangswahrscheinlichkeiten 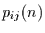 können zu einer
Übergangsmatrix
können zu einer
Übergangsmatrix 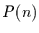 mit
mit
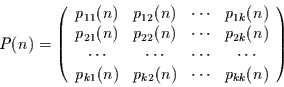 |
(3.4) |
zusammengefaßt werden. Solche Matrizen, mit Wahrscheinlichkeiten als
Elementen heißen stochastische Matrizen. Sie sind quadratisch, alle ihre
Elemente erfüllen die Eigenschaft
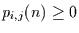 und alle Zeilensummen
sind gleich 1. Die letzte Eigenschaft ist eine Erhaltungseigenschaft, die
gewährleistet, daß sich die Realisation immer in einem Zustand
befindet. Mit Hilfe der Übergangsmatrix kann die zeitlichen Entwicklung des
Wahrscheinlichkeitsvektors geschrieben werden als
und alle Zeilensummen
sind gleich 1. Die letzte Eigenschaft ist eine Erhaltungseigenschaft, die
gewährleistet, daß sich die Realisation immer in einem Zustand
befindet. Mit Hilfe der Übergangsmatrix kann die zeitlichen Entwicklung des
Wahrscheinlichkeitsvektors geschrieben werden als
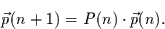 |
(3.5) |
Eine häufige Anwendung dieser Gleichung liegt darin, daß man damit
Wahrscheinlichkeitsprognosen durchführen kann. Meist ist ein Anfangszustand
gegeben, d.h. 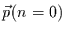 hat an einer Stelle eine 1 und sonst überall
0. Dann kann man mit Hilfe von Gleichung (3.5) prognostizieren, mit
welcher Wahrscheinlichkeit welche Zustände in der Zukunft eingenommen
werden.
hat an einer Stelle eine 1 und sonst überall
0. Dann kann man mit Hilfe von Gleichung (3.5) prognostizieren, mit
welcher Wahrscheinlichkeit welche Zustände in der Zukunft eingenommen
werden.
Unterabschnitte



Nächste Seite: Homogene Markovketten und Chapman-Kolmogoroff-Gleichung
Aufwärts: Symbolische Dynamik, Punktprozesse und
Vorherige Seite: Betrachtung bei diskreten Zeitschritten
Inhalt
ich
2000-01-24