


Nächste Seite: Markovketten
Aufwärts: Nichtkonstante Ereigniswahrscheinlichkeitsdichten
Vorherige Seite: Change-Point Punktprozesse
Inhalt
Wir betrachten nun die Zeit in diskreten Schritten
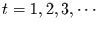 .
Die Wahrscheinlichkeit für das Eintreten eines Ereignisses zur Zeit
.
Die Wahrscheinlichkeit für das Eintreten eines Ereignisses zur Zeit 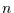 ist dann
ist dann 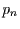 . Das Ereignis tritt dann im Zeitschritt
. Das Ereignis tritt dann im Zeitschritt 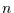 mit der
Wahrscheinlichkeit
mit der
Wahrscheinlichkeit 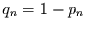 nicht ein. Wir fragen zunächst wieder
allgemein nach der Wahrscheinlichkeit dafür, daß
nicht ein. Wir fragen zunächst wieder
allgemein nach der Wahrscheinlichkeit dafür, daß
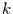 Ereignisse in den
Ereignisse in den 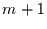 Zeitschritten von
Zeitschritten von 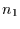 bis
bis 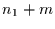 stattfinden und gehen dazu sukzessive vor. Die Wahrscheinlichkeit kein
Ereignis vorzufinden ist offensichtlich
stattfinden und gehen dazu sukzessive vor. Die Wahrscheinlichkeit kein
Ereignis vorzufinden ist offensichtlich
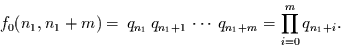 |
(2.42) |
Die Wahrscheinlichkeit ein Ereignis vorzufinden ergibt sich daraus, daß an
einer beliebigen Stelle 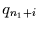 durch
durch 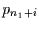 ersetzt werden muß.
Da jede Stelle im Intervall
ersetzt werden muß.
Da jede Stelle im Intervall 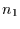 bis
bis 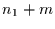 dafür in Frage kommt,
entstehen
dafür in Frage kommt,
entstehen 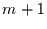 Terme. Es folgt also
Terme. Es folgt also
![\begin{displaymath}
\begin{array}{rcl}
f_{1}(n_{1},n_{1}+m) & = &
\, p_{n_{1}...
...s_{{i=0 \atop i\neq j}}^{m}q_{n_{1}+m}
\right].
\end{array}
\end{displaymath}](img134.gif) |
(2.43) |
Für den Spezialfall, daß die Eintrittswahrscheinlichkeiten alle gleich
sind (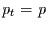 ), folgt daraus wieder das Ergebnis des Bernoulli-Experiments
(s. Gleichung (2.14))
für den Spezialfall
), folgt daraus wieder das Ergebnis des Bernoulli-Experiments
(s. Gleichung (2.14))
für den Spezialfall 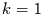 :
:
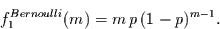 |
(2.44) |
Man kann sich leicht vorstellen, daß die allgemeinen Ausdrücke für
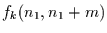 schon für kleine
schon für kleine 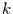 recht kompliziert werden.
Andererseits kann man sich bestimmte Strukturen von
recht kompliziert werden.
Andererseits kann man sich bestimmte Strukturen von 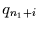 vorstellen, für die sich wiederum vereinfachte Ausdrücke ergeben.
So folgt z.B. aus der exponentiellen Abnahme der Wahrscheinlichkeit des
Nichteintretens des Ereignisses (das ist die zeitdiskrete Form des
exponentiellen Alterns)
vorstellen, für die sich wiederum vereinfachte Ausdrücke ergeben.
So folgt z.B. aus der exponentiellen Abnahme der Wahrscheinlichkeit des
Nichteintretens des Ereignisses (das ist die zeitdiskrete Form des
exponentiellen Alterns)
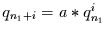
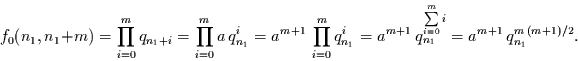 |
(2.45) |
Wir beenden nun die Betrachtungen von
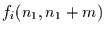 und wenden uns
der einfacheren Frage zu, wie lange man warten muß bis das erste Ereignis
eintritt. Die Wartezeit
und wenden uns
der einfacheren Frage zu, wie lange man warten muß bis das erste Ereignis
eintritt. Die Wartezeit 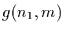 vom Zeitschritt
vom Zeitschritt
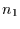 bis zum Zeitschritt mit dem ersten Ereignis
bis zum Zeitschritt mit dem ersten Ereignis
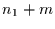 , ist gegeben durch das
Produkt der Wahrscheinlichkeit dafür, daß in der Zeit von
, ist gegeben durch das
Produkt der Wahrscheinlichkeit dafür, daß in der Zeit von 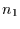 bis
bis
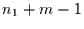 kein Ereignis stattgefunden hat und im Zeitschritt
kein Ereignis stattgefunden hat und im Zeitschritt 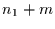 ein Ereignis stattfindet:
ein Ereignis stattfindet:
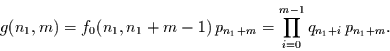 |
(2.46) |
Für den Fall 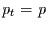 folgt daraus wieder die Wartezeitverteilung des
Bernoulli-Experiments
folgt daraus wieder die Wartezeitverteilung des
Bernoulli-Experiments
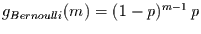 mit der mittleren
Wartezeit (= Wiederkehrzeit)
mit der mittleren
Wartezeit (= Wiederkehrzeit)
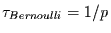 .
Für das zeitdiskrete exponentielle Altern
.
Für das zeitdiskrete exponentielle Altern
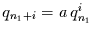 folgt durch Einsetzen von Gleichung (2.45) in Gleichung (2.46)
folgt durch Einsetzen von Gleichung (2.45) in Gleichung (2.46)
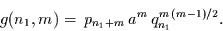 |
(2.47) |
Die Wiederkehrzeit in Abhängigkeit von 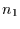 und
und 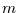 anzugeben, wird hier
erst garnicht versucht, sondern scheint eher ein Fall für numerische
Experimente zu sein.
Falls
anzugeben, wird hier
erst garnicht versucht, sondern scheint eher ein Fall für numerische
Experimente zu sein.
Falls 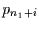 für alle
für alle 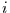 bekannt ist, kann im Prinzip
die Wartezeitverteilung
für jedes beliebige
bekannt ist, kann im Prinzip
die Wartezeitverteilung
für jedes beliebige 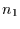 und
und 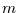 angegeben werden.
Ein Spezialfall soll hier noch vorgestellt werden, da er in der Klimatologie
von Bedeutung ist. Eine Variable sei Gauß-verteilt und stationär um einen
zeitabhängigen Mittelwert
angegeben werden.
Ein Spezialfall soll hier noch vorgestellt werden, da er in der Klimatologie
von Bedeutung ist. Eine Variable sei Gauß-verteilt und stationär um einen
zeitabhängigen Mittelwert 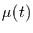 . Gesucht ist nun die Wartezeitverteilung
ab einem bestimmten Zeitpunkt
. Gesucht ist nun die Wartezeitverteilung
ab einem bestimmten Zeitpunkt 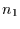 für das Überschreiten einer Schwelle
für das Überschreiten einer Schwelle
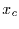 . Wegen
. Wegen
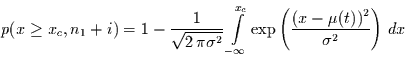 |
(2.48) |
folgt für die Wartezeitverteilung
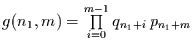 ein
Produkt aus
ein
Produkt aus 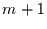 Errorfunktionen.
Errorfunktionen.



Nächste Seite: Markovketten
Aufwärts: Nichtkonstante Ereigniswahrscheinlichkeitsdichten
Vorherige Seite: Change-Point Punktprozesse
Inhalt
ich
2000-01-24
![\begin{displaymath}
\begin{array}{rcl}
f_{1}(n_{1},n_{1}+m) & = &
\, p_{n_{1}...
...s_{{i=0 \atop i\neq j}}^{m}q_{n_{1}+m}
\right].
\end{array}
\end{displaymath}](img134.gif)
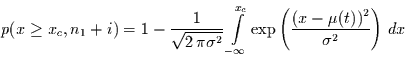
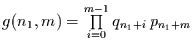 ein
Produkt aus
ein
Produkt aus