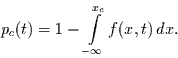


Nächste Seite: Wiederkehrzeit und Risiko
Aufwärts: Extremwerte
Vorherige Seite: Extremwerte
Inhalt
Man kann einen Extremwert 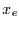 dadurch definieren, daß es ein Wert aus einer
kontinuierlichen oder diskreten Variable
dadurch definieren, daß es ein Wert aus einer
kontinuierlichen oder diskreten Variable 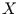 ist,
der eine vorgegebene Schwelle
ist,
der eine vorgegebene Schwelle
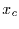 überschreitet (bzw. unterschreitet) und für den die
Eintrittswahrscheinlichkeit
überschreitet (bzw. unterschreitet) und für den die
Eintrittswahrscheinlichkeit
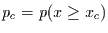 klein ist. Kennt man die
Wahrscheinlichkeitsdichte
klein ist. Kennt man die
Wahrscheinlichkeitsdichte 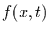 der Variablen
der Variablen 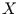 zur Zeit
zur Zeit 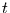 so folgt für
so folgt für 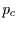
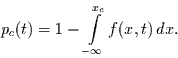 |
(1.1) |
Falls 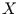 eine zeitkontinuierliche Variable ist, ist
eine zeitkontinuierliche Variable ist, ist 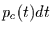 die
Wahrscheinlichkeitsdichte dafür, daß der Extremwert im Zeitintervall
die
Wahrscheinlichkeitsdichte dafür, daß der Extremwert im Zeitintervall
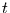 bis
bis 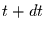 eintritt. Bei diskreter Zeitbetrachtung, gibt
eintritt. Bei diskreter Zeitbetrachtung, gibt 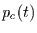 die
Wahrscheinlichkeit für das Eintreten eines Extremwertes im Zeitintervall
von
die
Wahrscheinlichkeit für das Eintreten eines Extremwertes im Zeitintervall
von 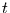 bis
bis 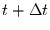 an. Man beachte, daß im zeitkontinuierlichen Fall
erst das Integral über
an. Man beachte, daß im zeitkontinuierlichen Fall
erst das Integral über 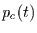 wieder eine Wahrscheinlichkeit ist.
Diese Unterscheidung wird uns noch öfter begegnen.
Gleichung (1.1) vereinfacht sich drastisch für stationäre Prozesse
ohne Gedächtnis (weisses Rauschen). Für den Fall von Gaußschem weißen
Rauschen mit der Standardabweichung 1 und dem Mittelwert 0 folgt
wieder eine Wahrscheinlichkeit ist.
Diese Unterscheidung wird uns noch öfter begegnen.
Gleichung (1.1) vereinfacht sich drastisch für stationäre Prozesse
ohne Gedächtnis (weisses Rauschen). Für den Fall von Gaußschem weißen
Rauschen mit der Standardabweichung 1 und dem Mittelwert 0 folgt
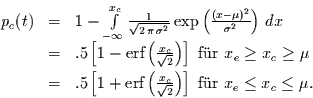 |
(1.2) |
Obwohl diese Gleichung mit Hilfe der Numerical Recipies leicht lösbar ist,
muß man auch in diesem einfachen Fall aufpassen, ob man sich für
Maxima, Minima oder beides interessiert.
Falls die Variable 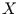 einer einfachen theoretisch beschreibbaren Verteilung
wie der eben verwendeten Gaußverteilung genügt, weiß,
aber instationär ist, in dem Sinn, daß Lage- und Streuparameter als
Funktionen der Zeit dargestellt werden können, kann die Integration von
Gleichung (1.1) immernoch durch Funktionen der Numerical Recipies
genähert werden.
Es gilt dann z.B. für daß varianz- und mittelwertinstationäre gaußsche
weiße Rauschen
einer einfachen theoretisch beschreibbaren Verteilung
wie der eben verwendeten Gaußverteilung genügt, weiß,
aber instationär ist, in dem Sinn, daß Lage- und Streuparameter als
Funktionen der Zeit dargestellt werden können, kann die Integration von
Gleichung (1.1) immernoch durch Funktionen der Numerical Recipies
genähert werden.
Es gilt dann z.B. für daß varianz- und mittelwertinstationäre gaußsche
weiße Rauschen
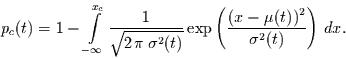 |
(1.3) |
Falls ein Prozeß Autokorrelation besitzt, kann er nicht mehr auf diese
Weise formuliert werden. Man muß dann Information über die
Vorgängerwerte berücksichtigen, denn dann ist 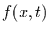 eine Funktion
der Verteilungen zu früheren Zeiten. Für wertdiskrete Reihen kann dies
durch eine Markov-Kette beschrieben werden.
eine Funktion
der Verteilungen zu früheren Zeiten. Für wertdiskrete Reihen kann dies
durch eine Markov-Kette beschrieben werden.



Nächste Seite: Wiederkehrzeit und Risiko
Aufwärts: Extremwerte
Vorherige Seite: Extremwerte
Inhalt
ich
2000-01-24