

Nächste Seite: Verteilung einer harmonisch schwingenden
Aufwärts: Woher kommt die U-Verteilung?
Vorherige Seite: Woher kommt die U-Verteilung?
In der Literatur findet man zwei Darstellungsformen der U-Verteilung.
Einerseits kann die U-Verteilung zwischen 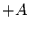 und
und 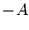 angegeben werden, dann
gilt für die Wahrscheinlichkeitsdichte
angegeben werden, dann
gilt für die Wahrscheinlichkeitsdichte
![\begin{displaymath}
f(x)=\left\{
\begin{array}{ll}
\frac{1}{\pi}\left(A^{2}-x...
...\le A \\ [1ex]
0 & \mbox{, sonst.}
\end{array}
\right.
\end{displaymath}](img4.gif) |
(1) |
Andererseits findet man auch eine zwischen 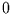 und
und 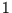 definierte U-Verteilung,
für die dann die Dichte
definierte U-Verteilung,
für die dann die Dichte
![\begin{displaymath}
g(z)=\left\{
\begin{array}{ll}
\frac{1}{\pi}\left(z(1-z)\...
...\le 1 \\ [1ex]
0 & \mbox{, sonst.}
\end{array}
\right.
\end{displaymath}](img7.gif) |
(2) |
angegeben wird.
Man kann sich leicht vergewissern, daß sowohl Gleichung (1) als auch
Gleichung (2) Wahrscheinlichkeitsdichten beschreiben,
da sie nirgends negativ
sind und das Integral von 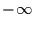 bis
bis 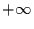 über diese Dichten jeweils
über diese Dichten jeweils
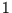 ergibt.
Zunächst soll hier gezeigt werden, daß die beiden Dichten sich nur darin
unterscheiden, daß sie auf verschiedenen Intervallen definiert sind, d.h. daß
sie bis auf einen Normierungsfaktor die gleiche Form haben. Dazu
wird das Intervall
ergibt.
Zunächst soll hier gezeigt werden, daß die beiden Dichten sich nur darin
unterscheiden, daß sie auf verschiedenen Intervallen definiert sind, d.h. daß
sie bis auf einen Normierungsfaktor die gleiche Form haben. Dazu
wird das Intervall ![$[-A,A]$](img10.gif) in das Intervall [0,1] transformiert. Dies
geschieht durch die Transformation
in das Intervall [0,1] transformiert. Dies
geschieht durch die Transformation
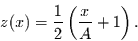 |
(3) |
Nun kann Gleichung (3) in Gleichung (2) eingesetzt werden, woraus
folgt
![\begin{displaymath}
\begin{array}{rcl}
g(z) & = & \frac{1}{\pi} \left[\left(
...
...x]
& = & \frac{\partial z}{\partial x}\, f(x).
\end{array}
\end{displaymath}](img12.gif) |
(4) |
Der Faktor 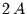 , um den
, um den 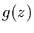 gegenüber
gegenüber 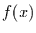 verstärkt ist, ist gleich
dem Faktor, um den
verstärkt ist, ist gleich
dem Faktor, um den 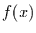 breiter ist als
breiter ist als 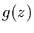 . Er folgt damit nur daraus, daß
das Integral über beide Funktionen
. Er folgt damit nur daraus, daß
das Integral über beide Funktionen 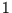 sein muß. Die beiden Verteilungen sind
also gleich. Doch wo kommen sie her?
sein muß. Die beiden Verteilungen sind
also gleich. Doch wo kommen sie her?


Nächste Seite: Verteilung einer harmonisch schwingenden
Aufwärts: Woher kommt die U-Verteilung?
Vorherige Seite: Woher kommt die U-Verteilung?
ich
2000-01-24
![\begin{displaymath}
f(x)=\left\{
\begin{array}{ll}
\frac{1}{\pi}\left(A^{2}-x...
...\le A \\ [1ex]
0 & \mbox{, sonst.}
\end{array}
\right.
\end{displaymath}](img4.gif)
![\begin{displaymath}
\begin{array}{rcl}
g(z) & = & \frac{1}{\pi} \left[\left(
...
...x]
& = & \frac{\partial z}{\partial x}\, f(x).
\end{array}
\end{displaymath}](img12.gif)