Verteilung einer harmonisch schwingenden
Zeitreihe

Eine harmonisch schwingende Zeitreihe ist gegeben durch

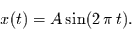$$x(t)=A \sin(2\,\pi\,t).$$ (5)

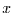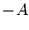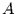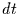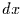Um die Verteilung der Variable $x$ zu erhalten (die von $-A$ und $A$ begrenzt ist), muß man berechnen, welchen Anteil der Zeit $dt$ die Variable in einem Intervall $dx$ verbringt. Dazu stellt man Gleichung (5) zunächst nach 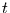$t$ um und erhält

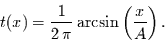$$t(x) = \frac{1}{2\,\pi} \arcsin\left(\frac{x}{A}\right).$$ (6)

Die Ableitung davon ist die noch nicht normierte Wahrscheinlichkeitsdichte

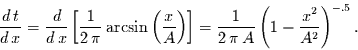$$\frac{d\,t}{d\,x} =\frac{d}{d\,x}\left[ \frac{1}{2\,\pi} \a... ...ac{1}{2\,\pi\,A} \left(1- \frac{x^{2}}{A^{2}}\right)^{-.5}.$$ (7)

Für die Wahrscheinlichkeitsdichte folgt dann schließlich

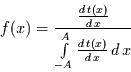$$f(x)=\frac{\frac{d\,t(x)}{d\,x}}{\int\limits_{-A}^{A}\frac{d\,t(x)}{d\,x}\,d\,x}$$ (8)

mit

$$\begin{array}{rcl} \int\limits_{-A}^{A}\frac{d\,t(x)}{d\,x... ...i}{2} + \frac{\pi}{2}\right] = \frac{1}{2}. \end{array}$$ (9)

Damit ist die Wahrscheinlichkeitsdichte für die Verteilung einer harmonisch schwingenden Zeitreihe mit der Amplitude 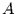$A$ gegeben durch

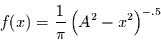$$f(x) = \frac{1}{\pi}\left(A^{2}-x^{2}\right)^{-.5}$$ (10)

was mit Gleichung (1) identisch ist. Eine harmonisc hschwingende Zeitreihe ist also U-verteilt. Für die Wahrscheinlichkeitsfunktion folgt dann

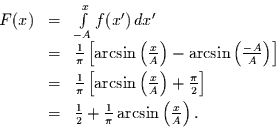$$\begin{array}{rcl} F(x) & = & \int\limits_{-A}^{x} f(x')\,... ...\frac{1}{\pi} \arcsin\left(\frac{x}{A}\right). \end{array}$$ (11)