

Nächste Seite: Erzeugung U-verteilter Zufallszahlen
Aufwärts: Woher kommt die U-Verteilung?
Vorherige Seite: Verteilung einer harmonisch schwingenden
Die Feigenbaumdynamik ist gegeben durch
![\begin{displaymath}
x_{n+1} = r\, x_{n}\,(1 - x_{n}), \mbox{ mit }x_{0}\in[0,1].
\end{displaymath}](img28.gif) |
(12) |
Für den Fall 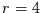 spricht man von vollentwickeltem Chaos, und genau für diesen
Fall soll hier die Verteilung der Variablen
spricht man von vollentwickeltem Chaos, und genau für diesen
Fall soll hier die Verteilung der Variablen 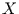 berechnet werden. Man könnte
dazu das Intervall
berechnet werden. Man könnte
dazu das Intervall ![$[0,1]$](img30.gif) partitionieren (z.B. in
partitionieren (z.B. in 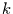 gleichgroße Klasssen
einteilen) und zählen, wie oft die nach Gleichung (12) Iterierte in jeder
Klasse vorbeikommt. Dies würde zumindest zu einer numerischen Näherung der
Verteilung führen. Hier soll die Verteilung aber anlaytisch berechnet werden.
Dazu wird die Feigenbaumdynamik auf die Zeltdachabbildung
gleichgroße Klasssen
einteilen) und zählen, wie oft die nach Gleichung (12) Iterierte in jeder
Klasse vorbeikommt. Dies würde zumindest zu einer numerischen Näherung der
Verteilung führen. Hier soll die Verteilung aber anlaytisch berechnet werden.
Dazu wird die Feigenbaumdynamik auf die Zeltdachabbildung
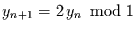 zurückgeführt, was durch die Transformation
zurückgeführt, was durch die Transformation
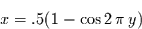 |
(13) |
geschieht. Da die Rechnung in mehreren Schritten
verläuft, soll sie hier vorgeführt werden:
![\begin{displaymath}
\begin{array}{rcl}
x_{n+1} & = & r\,x_{n} \,(1-x_{n}) \\ [...
...{n})]\\ [1ex]
y_{n+1} & = & 2\,y_{n} \bmod 1.
\end{array}
\end{displaymath}](img34.gif) |
(14) |
Nun ist diese Zeltdachabbildung zwischen 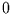 und
und 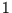 gleichverteilt. Betrachtet
man andererseits die harmonisch schwingende Zeitreihe,
so reicht es aus, genau eine Schwingung zu untersuchen. Dabei läuft die Zeit
gleichverteilt. Betrachtet
man andererseits die harmonisch schwingende Zeitreihe,
so reicht es aus, genau eine Schwingung zu untersuchen. Dabei läuft die Zeit
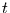 gleichmäßig von
gleichmäßig von 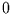 bis
bis 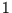 . Sie ist also ebenfalls
zwischen
. Sie ist also ebenfalls
zwischen 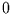 und
und 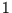 gleichverteilt
(wenn auch nicht zufällig). Die harmonische Schwingung ist dann proportional
zu
gleichverteilt
(wenn auch nicht zufällig). Die harmonische Schwingung ist dann proportional
zu
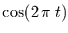 und transformiert damit die gleichverteilte Variable
und transformiert damit die gleichverteilte Variable 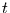 in die U-verteilte Variable
in die U-verteilte Variable 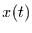 aus Gleichung (5).
Genau das Gleiche geschieht durch Gleichung (13). Sie transformiert
die gleichverteilte Variable der Zeltdachabbildung in die U-verteilte Variable
der Feigenbaumabbildung bei
aus Gleichung (5).
Genau das Gleiche geschieht durch Gleichung (13). Sie transformiert
die gleichverteilte Variable der Zeltdachabbildung in die U-verteilte Variable
der Feigenbaumabbildung bei 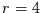 . Es ist demnach offensichtlich, daß die
trigonometrischen Funktionen
. Es ist demnach offensichtlich, daß die
trigonometrischen Funktionen
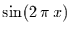 und
und
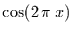 gleichverteilte
Variablen in U-vertelte Variablen transformieren.
gleichverteilte
Variablen in U-vertelte Variablen transformieren.


Nächste Seite: Erzeugung U-verteilter Zufallszahlen
Aufwärts: Woher kommt die U-Verteilung?
Vorherige Seite: Verteilung einer harmonisch schwingenden
ich
2000-01-24