

Nächste Seite: Transformation der Verteilungen
Aufwärts: Zur zeitlichen Analyse von
Vorherige Seite: Zur zeitlichen Analyse von
Mit Hilfe der klassischen Zeitreihenanalyse kann man
regelhaftes Verhalten (strukturierte Komponenten)
in Zeitreihen erkennen und separieren. Solche strukturierten
Komponenten sind z.B. Trends und Jahresgang,
sowie Änderungen im Jahresgang und weitere harmonische und glatte Anteile.
Wenn es einem gelingt alle strukturierten Komponenten
zu separieren, erhält man als Rest ein Rauschen. Dieses Rauschen muß dann
mittelwertstationär sein, da die Variationen des Mittelwertes durch die
strukturierten Komponenten beschrieben werden.
Keinesfalls allerdings muß das Residuum varianzstationär sein. Deshalb soll
nun die zeitliche Struktur der Varianz (bzw. etwas allgemeiner der Variationen)
untersucht werden.
Dazu wird davon ausgegangen, daß die Variationen Gauß-verteilt sind
1. Nun können die
Variationen selbst strukturierte Komponenten, wie z.B.
einen Jahresgang, einen Trend und eine
Änderung des Jahresgangs aufweisen. Diese gilt es zu detektieren und zu
beschreiben. Dabei tritt das Problem auf, daß die Abweichungen vom Mittelwert
nicht direkt als Variable verwendet werden können, da diese ja um den
Mittelwert zentriert sind. Deshalb stehen verschiedene Möglichkeiten der
Transformation der Abweichungen zur Verfügung. So könnte man z.B. den Betrag
der Abweichungen untersuchen, der, wie wir sehen werden, 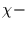 verteilt ist
mit einem Freiheitsgrad. Oder man könnte das Quadrat der Abweichungen
wählen, was zu einer
verteilt ist
mit einem Freiheitsgrad. Oder man könnte das Quadrat der Abweichungen
wählen, was zu einer 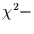 verteilten Variable führt, die wiederum einen
Freiheitsgrad hat. Beide Verteilungen sind der Gauß-Verteilung nicht einmal
ähnlich, weshalb dann die Anwendung der Methode der kleinsten Quadrate nicht
mehr in Frage kommt. Andere (sogenannte robuste) Verfahren, kämen dann zwar
für
die Analyse in Frage, aber sie unterliegen einer gewissen Willkür des
Anwenders. Sie sind daher eher geeignet, Strukturen in nicht Gauß-verteilten
Zeitreihen zu erkennen, als diese objektiv
zu beschreiben. Deshalb soll hier ein
anderer Weg eingeschlagen werden, indem versucht wird, die Abweichungen in
zumindest Gauß-ähnliche Verteilungen zu transformieren. Gauß-ähnlich
soll dabei bedeuten, daß man auf Grund des zur Verfügung stehenden
Datenmaterials die Verteilung nicht signifikant von einer Gauß-Verteilung
unterscheiden kann.
Entsprechend dem zentralen Grenzwertsatz ist die Mittelung ein Weg, eine
Verteilung in eine Gauß-ähnliche Verteilung zu transformieren. Daher
erscheint es naheliegend, die Zeitreihe von gleitenden Mitteln quadrierter
Abstände (gleitende Varianzen) zu untersuchen. Je größer dabei das
Datenfenster ist, für das man die Varianz berechnet, umso ähnlicher ist
die entstehende
verteilten Variable führt, die wiederum einen
Freiheitsgrad hat. Beide Verteilungen sind der Gauß-Verteilung nicht einmal
ähnlich, weshalb dann die Anwendung der Methode der kleinsten Quadrate nicht
mehr in Frage kommt. Andere (sogenannte robuste) Verfahren, kämen dann zwar
für
die Analyse in Frage, aber sie unterliegen einer gewissen Willkür des
Anwenders. Sie sind daher eher geeignet, Strukturen in nicht Gauß-verteilten
Zeitreihen zu erkennen, als diese objektiv
zu beschreiben. Deshalb soll hier ein
anderer Weg eingeschlagen werden, indem versucht wird, die Abweichungen in
zumindest Gauß-ähnliche Verteilungen zu transformieren. Gauß-ähnlich
soll dabei bedeuten, daß man auf Grund des zur Verfügung stehenden
Datenmaterials die Verteilung nicht signifikant von einer Gauß-Verteilung
unterscheiden kann.
Entsprechend dem zentralen Grenzwertsatz ist die Mittelung ein Weg, eine
Verteilung in eine Gauß-ähnliche Verteilung zu transformieren. Daher
erscheint es naheliegend, die Zeitreihe von gleitenden Mitteln quadrierter
Abstände (gleitende Varianzen) zu untersuchen. Je größer dabei das
Datenfenster ist, für das man die Varianz berechnet, umso ähnlicher ist
die entstehende 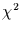 -Verteilung der Gauß-Verteilung, aber umso mehr
Information über die Variabilität der Varianz geht dabei verloren.
Man möchte also ein möglichst schmales Datenfenster verwenden, um
möglichst wenig Information zu verlieren.
Um hier ein optimales Maß für die Länge des Datenfensters
zur Berechnung gleitender Varianzen (oder womöglich sinnvollerer Maße der
Variation) zu finden, ist es zunächst
notwendig, sich mit der Transformation von Verteilungen zu beschäftigen.
Dies ist der Inhalt des nächsten Abschnitts.
-Verteilung der Gauß-Verteilung, aber umso mehr
Information über die Variabilität der Varianz geht dabei verloren.
Man möchte also ein möglichst schmales Datenfenster verwenden, um
möglichst wenig Information zu verlieren.
Um hier ein optimales Maß für die Länge des Datenfensters
zur Berechnung gleitender Varianzen (oder womöglich sinnvollerer Maße der
Variation) zu finden, ist es zunächst
notwendig, sich mit der Transformation von Verteilungen zu beschäftigen.
Dies ist der Inhalt des nächsten Abschnitts.


Nächste Seite: Transformation der Verteilungen
Aufwärts: Zur zeitlichen Analyse von
Vorherige Seite: Zur zeitlichen Analyse von
ich
2000-01-25