

Nächste Seite: -Verteilung
Aufwärts: Zur zeitlichen Analyse von
Vorherige Seite: Ziel
Um die Transformationsbeziehung für die Verteilungen zweier funktional
voneinander abhängigen Zufallsvariablen herzuleiten, gehen wir von
einer Zufallsvariable 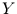 aus, die über eine bijektive Funktion
aus, die über eine bijektive Funktion 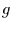 von
der Zufallsvariable
von
der Zufallsvariable 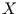 abhängt. Die Bijektivität ist dabei eine
notwendige Bedingung, um eine eindeutige umgekehrte Funktion
abhängt. Die Bijektivität ist dabei eine
notwendige Bedingung, um eine eindeutige umgekehrte Funktion
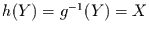 angeben zu können2.
Ziel ist es nun aus der Kenntnis der
Funktion
angeben zu können2.
Ziel ist es nun aus der Kenntnis der
Funktion 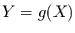 und der Wahrscheinlichkeitsdichte
und der Wahrscheinlichkeitsdichte 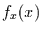 der Variable
der Variable
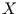 auf die Wahrscheinlichkeitsdichte
auf die Wahrscheinlichkeitsdichte 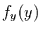 der Variable
der Variable 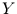 zu
schließen. Für die Wahrscheinlichkeitsverteilungen der beiden Variablen
soll gelten
zu
schließen. Für die Wahrscheinlichkeitsverteilungen der beiden Variablen
soll gelten
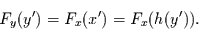 |
(1) |
Das bedeutet, daß es zu jedem Wert 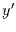 einen Wert
einen Wert 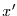 gibt, so daß
die Wahrscheinlichkeit dafür, daß die Variable
gibt, so daß
die Wahrscheinlichkeit dafür, daß die Variable 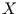 einen Wert kleiner als
einen Wert kleiner als
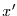 annimmt, gleich der Wahrscheinlichkeit ist, daß die Variable
annimmt, gleich der Wahrscheinlichkeit ist, daß die Variable 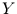 einen
Wert kleiner
einen
Wert kleiner 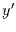 annimmt. Um die Wahrscheinlichkeitsdichte von
annimmt. Um die Wahrscheinlichkeitsdichte von 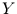 zu
erhalten, wird Gleichung (1) nun nach
zu
erhalten, wird Gleichung (1) nun nach 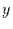 abgeleitet. Man erhält
nach der Kettenregel
abgeleitet. Man erhält
nach der Kettenregel
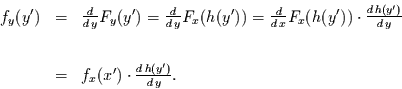 |
(2) |
Mit Hilfe dieser Gleichung ist es möglich, aus der Kenntnis der funktionalen
Abhängigkeit einer Variablen 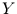 von einer Variablen
von einer Variablen 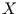 und der
Wahrscheinlichkeitsdichte der Variablen
und der
Wahrscheinlichkeitsdichte der Variablen 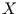 , auf die Wahrscheinlichkeitsdichte
der Variablen
, auf die Wahrscheinlichkeitsdichte
der Variablen 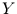 zu schließen.
zu schließen.


Nächste Seite: -Verteilung
Aufwärts: Zur zeitlichen Analyse von
Vorherige Seite: Ziel
ich
2000-01-25