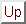

Nächste Seite: -Verteilung
Aufwärts: Zur zeitlichen Analyse von
Vorherige Seite: Transformation der Verteilungen
Die Summe von 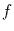 unabhängigen quadrierten normalverteilten Zufallsvariablen
unabhängigen quadrierten normalverteilten Zufallsvariablen
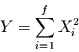 |
(3) |
ist  -verteilt mit
-verteilt mit 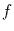 Freiheitsgraden.
Für den Fall
Freiheitsgraden.
Für den Fall 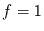 soll nun die Wahrscheinlichkeitsdichte von
soll nun die Wahrscheinlichkeitsdichte von 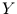 hergeleitet
werden. Es gilt also
hergeleitet
werden. Es gilt also 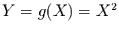 . Diese Abbildung ist nicht bijektiv, so
daß die oben angegebene Gleichung (2) nicht verwendet werden kann.
Als Verallgemeinerung von Gleichung (2) kann man in diesem Fall
aber schreiben
. Diese Abbildung ist nicht bijektiv, so
daß die oben angegebene Gleichung (2) nicht verwendet werden kann.
Als Verallgemeinerung von Gleichung (2) kann man in diesem Fall
aber schreiben
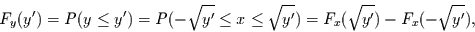 |
(4) |
d.h. die Wahrscheinlichkeit dafür, daß 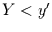 ist, ist gleich der
Wahrscheinlichkeit dafür, daß
ist, ist gleich der
Wahrscheinlichkeit dafür, daß 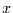 zwischen
zwischen 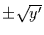 liegt.
Dann gilt weiter
liegt.
Dann gilt weiter
![\begin{displaymath}
\begin{array}{rcl}
f_{y}(y') & = &
\frac{d}{d\, y}F_{x}(...
...[
f_{x}(\sqrt{y'}+f_{x}(-\sqrt{y'})
\right].
\end{array}
\end{displaymath}](img28.gif) |
(5) |
Für eine Gauß-verteilte Variable 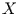 ist
ist 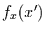 nun symmetrisch und
es gilt
nun symmetrisch und
es gilt
Dann folgt für die  -verteilte Variable mit einem Freiheitsgrad
-verteilte Variable mit einem Freiheitsgrad
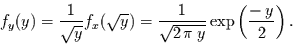 |
(6) |
Für die  -Verteilung mit mehreren Freiheitsgraden kann man auf
ähnliche Weise die Form der Wahrscheinlichkeitsdichte herleiten. Sie
soll hier aber nur als Ergebnis dargestellt werden. Für
-Verteilung mit mehreren Freiheitsgraden kann man auf
ähnliche Weise die Form der Wahrscheinlichkeitsdichte herleiten. Sie
soll hier aber nur als Ergebnis dargestellt werden. Für 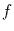 Freiheitsgrade
hat die
Freiheitsgrade
hat die  -Verteilung (Wahrscheinlichkeitsdichte) die Form
-Verteilung (Wahrscheinlichkeitsdichte) die Form
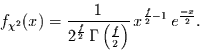 |
(7) |
Die Werte der Gamma-Funktion folgen dabei aus den drei Gleichungen
Um nun die  -Verteilung bei beliebig vielen Freiheitsgraden mit der
Gauß-Verteilung vergleichen zu können, benötigen wir noch
die Momente der Verteilung.
Für das
-Verteilung bei beliebig vielen Freiheitsgraden mit der
Gauß-Verteilung vergleichen zu können, benötigen wir noch
die Momente der Verteilung.
Für das 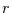 -te Moment
-te Moment  der
der  -Verteilung gilt allgemein
-Verteilung gilt allgemein
 |
(8) |
Für den Erwartungswert 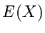 und die Varianz
und die Varianz 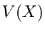 gilt
gilt
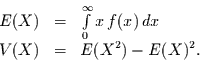 |
(9) |
Dann folgt mit Gleichung(8) für den Erwartungswert
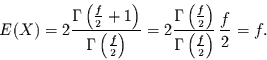 |
(10) |
Für das zweite Moment der  -Verteilung folgt
-Verteilung folgt
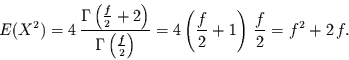 |
(11) |
Damit folgt für die Varianz der  -Verteilung
-Verteilung
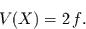 |
(12) |
Durch die Kenntnis von Erwartungswert und Varianz der
 -Verteilung für beliebige
Freiheitsgrade sind wir in der Lage,
diese mit der Gauß-Verteilung bei gleichem Mittelwert und gleicher
Varianz optisch zu vergleichen. Dazu sind in Abbildung 1 sowohl die
-Verteilung für beliebige
Freiheitsgrade sind wir in der Lage,
diese mit der Gauß-Verteilung bei gleichem Mittelwert und gleicher
Varianz optisch zu vergleichen. Dazu sind in Abbildung 1 sowohl die
 -Verteilung, als auch die Gauß-Verteilung mit gleichem
Mittelwert und gleicher Varianz für 10, 20 und 30 Freiheitsgrade
eingezeichnet.
-Verteilung, als auch die Gauß-Verteilung mit gleichem
Mittelwert und gleicher Varianz für 10, 20 und 30 Freiheitsgrade
eingezeichnet.
Abbildung:
Vergleich von  -Verteilung (durchgezogene
Linie) und Gauß-Verteilung (unterbrochene Linie)
mit gleichem Mittelwert und gleicher Varianz bei 10, 20 und 30 Freiheitsgraden.
-Verteilung (durchgezogene
Linie) und Gauß-Verteilung (unterbrochene Linie)
mit gleichem Mittelwert und gleicher Varianz bei 10, 20 und 30 Freiheitsgraden.
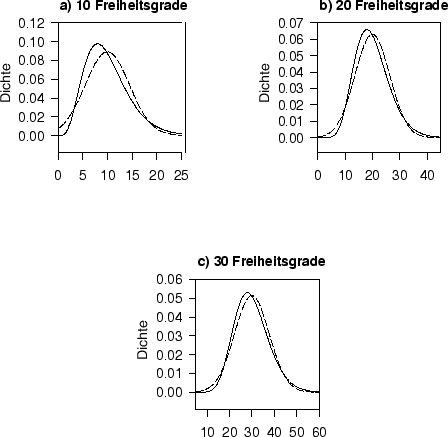 |
Zwar sieht man in Abb. 1, daß die  -Verteilung mit
zunehmenden Freiheitsgraden der Gauß-Verteilung immer ähnlicher
wird3, aber
dennoch sieht man auch bei 30 Freiheitsgraden noch deutliche Unterschiede.
In einem nächsten Schritt geht es nun darum, ein Maß für den Unterschied
zu finden. Dazu wird verglichen, ob Schiefe
-Verteilung mit
zunehmenden Freiheitsgraden der Gauß-Verteilung immer ähnlicher
wird3, aber
dennoch sieht man auch bei 30 Freiheitsgraden noch deutliche Unterschiede.
In einem nächsten Schritt geht es nun darum, ein Maß für den Unterschied
zu finden. Dazu wird verglichen, ob Schiefe 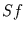 und Exzeß
und Exzeß 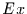 der
der
 -Verteilung mit
-Verteilung mit 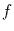 Freiheitsgraden, sich signifikant von der
Schiefe und dem Exzess der zugeordneten Gauß-Verteilung unterscheiden.
Der Erwartungswert der Schiefe
und des Exzesses ist bei der Gauß-Verteilung gleich null. Analysiert man eine
Gauß-verteilte Zeitreihe, so erhält man allerdings von null abweichende
Werte. Die Standardabweichung der Streuung der Schätzwerte von Schiefe und
Exzeß einer Gauß-verteilten Variable
hängt dabei von der Zeitreihenlänge
Freiheitsgraden, sich signifikant von der
Schiefe und dem Exzess der zugeordneten Gauß-Verteilung unterscheiden.
Der Erwartungswert der Schiefe
und des Exzesses ist bei der Gauß-Verteilung gleich null. Analysiert man eine
Gauß-verteilte Zeitreihe, so erhält man allerdings von null abweichende
Werte. Die Standardabweichung der Streuung der Schätzwerte von Schiefe und
Exzeß einer Gauß-verteilten Variable
hängt dabei von der Zeitreihenlänge 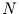 ab und geht für große
ab und geht für große 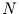 gegen null. Es gilt
gegen null. Es gilt
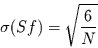 |
(13) |
und
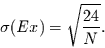 |
(14) |
Dabei konvergieren die Schätzer für Schiefe und Exzeß selbst gegen
Gauß-verteilte Variable. Wir sind damit in der Lage für beliebige
Zeitreihenlängen Konfidenzintervalle für 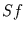 und
und 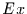 anzugeben. Werden diese
von einem Schätzwert überschritten, so hat man die Wahrscheinlichkeit dafür,
daß die Zeitreihe nicht aus einer Gauß-verteilten Variable stammt.
Mit Hilfe der Gleichung (10) und den Definitionen von Schiefe und
Exzeß
anzugeben. Werden diese
von einem Schätzwert überschritten, so hat man die Wahrscheinlichkeit dafür,
daß die Zeitreihe nicht aus einer Gauß-verteilten Variable stammt.
Mit Hilfe der Gleichung (10) und den Definitionen von Schiefe und
Exzeß
![\begin{displaymath}
\begin{array}{rcl}
Sf & = & \frac{E\left[(X-E(X))^{3}\righ...
...frac{E\left[(X-E(X))^{4}\right]}{\sigma^{4}}-3
\end{array}
\end{displaymath}](img48.gif) |
(15) |
folgt
![\begin{displaymath}
\begin{array}{rcl}
Sf(\chi^{2}) & = & \sqrt{\frac{8}{f}}\\ [2ex]
Ex(\chi^{2}) & = & \frac{12}{f}.
\end{array}
\end{displaymath}](img49.gif) |
(16) |
Wir sind nun in der Lage, zu testen, ob sich Schiefe und Exzeß einer
 -verteilten Zufallsvariable mit
-verteilten Zufallsvariable mit 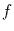 Freiheitsgraden signifikant
von Schiefe und Exzeß
einer Gauß-verteilten Zeitreihe der Länge
Freiheitsgraden signifikant
von Schiefe und Exzeß
einer Gauß-verteilten Zeitreihe der Länge 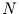 unterscheidet.
Damit kann die Frage geklärt werden, ob sich eine Zeitreihe von berechneten
Varianzen signifikant von einer gleichlangen Gauß-verteilten Zeitreihe
unterscheidet. Die Freiheitsgrade
unterscheidet.
Damit kann die Frage geklärt werden, ob sich eine Zeitreihe von berechneten
Varianzen signifikant von einer gleichlangen Gauß-verteilten Zeitreihe
unterscheidet. Die Freiheitsgrade 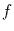 sind dabei die Anzahl der Werte die
in die Berechnung der Varianz eingehen. Abbildung 2 zeigt
den Verlauf von Schiefe und Exzeß einer
sind dabei die Anzahl der Werte die
in die Berechnung der Varianz eingehen. Abbildung 2 zeigt
den Verlauf von Schiefe und Exzeß einer  -verteilten Zufallsvariable
in Abhängigkeit von den Freiheitsgraden und den Verlauf von Konfidenzintervallen
von Schiefe und Exzeß einer Gauß-verteilten Zeitreihe in Abhängigkeit von
der Länge der Zeitreihe.
-verteilten Zufallsvariable
in Abhängigkeit von den Freiheitsgraden und den Verlauf von Konfidenzintervallen
von Schiefe und Exzeß einer Gauß-verteilten Zeitreihe in Abhängigkeit von
der Länge der Zeitreihe.
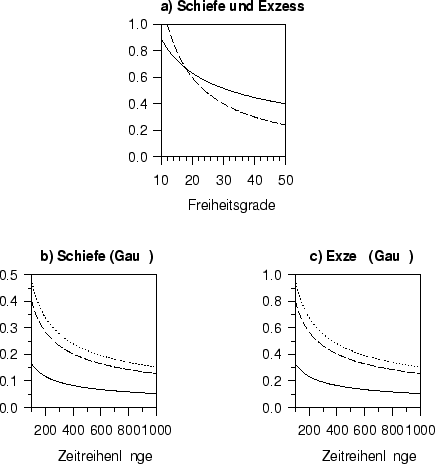
Abbildung:
a) Schiefe (durchgezogene Linie) und Exzeß (unterbrochene Linie)
einer  verteilten Zufallsvariable
in Abhängigkeit von der Anzahl der Freiheitsgrade.
b) Verlauf des 50% (durchgezogene Linie) , 90% (unterbrochene Linie) und
95% Konfidenzintervalls (gepunktete Linie) der Schiefe einer Gauß-verteilten
Zeitreihe in Abhängigkeit von deren Länge.
c) Verlauf des 50% (durchgezogene Linie), 90% (unterbrochene Linie) und
95% Konfidenzintervalls (gepunktete Linie)
des Exzesses einer Gauß-verteilten
Zeitreihe in Abhängigkeit von deren Länge.
verteilten Zufallsvariable
in Abhängigkeit von der Anzahl der Freiheitsgrade.
b) Verlauf des 50% (durchgezogene Linie) , 90% (unterbrochene Linie) und
95% Konfidenzintervalls (gepunktete Linie) der Schiefe einer Gauß-verteilten
Zeitreihe in Abhängigkeit von deren Länge.
c) Verlauf des 50% (durchgezogene Linie), 90% (unterbrochene Linie) und
95% Konfidenzintervalls (gepunktete Linie)
des Exzesses einer Gauß-verteilten
Zeitreihe in Abhängigkeit von deren Länge.
 |
Mit Hilfe der Gleichungen (13) und (14) und der Annahme,
daß Schiefe und Exzeß Gaußverteilte Schätzer sind, folgt das
90%-Konfidenzintervall durch Multiplikation der Standardabweichung dieser
Schätzer mit 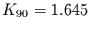 und das 95%-Konfidenzintervall durch den
Faktor
und das 95%-Konfidenzintervall durch den
Faktor 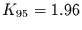 . Man kann nun fragen, wie kurz eine Reihe von
. Man kann nun fragen, wie kurz eine Reihe von
 -verteilten Werten mit
-verteilten Werten mit 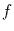 Freiheitsgraden sein muß, um noch nicht
von einer Gauß-verteilten Variable unterscheidbar zu sein.
Dazu kann die Schiefe der
Freiheitsgraden sein muß, um noch nicht
von einer Gauß-verteilten Variable unterscheidbar zu sein.
Dazu kann die Schiefe der  -Verteilung mit dem Konfidenzintervall der
Schiefe der Gauß-Verteilung gleichgesetzt werden. Man erhält für das
90%-Niveau
-Verteilung mit dem Konfidenzintervall der
Schiefe der Gauß-Verteilung gleichgesetzt werden. Man erhält für das
90%-Niveau
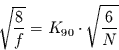 |
(17) |
und demnach
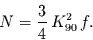 |
(18) |
Analog erhält man für den Exzeß
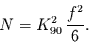 |
(19) |
Für 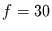 Freiheitsgrade unterscheidet sich die Schiefe einer
Freiheitsgrade unterscheidet sich die Schiefe einer  -verteilten
Variable schon ab 61 Werten signifikant von einer gleichlangen Gauß-Verteilung.
Der Exzeß ist erst ab 406 Werten signifikant zu unterscheiden.
Daraus muß geschlossen werden, daß die Analyse von Zeitreihen gleitender
Varianzen nicht mit der Methode der kleinsten Quadrate durchgeführt werden
kann, denn man muß einerseits über einen möglichst großen Zeitraum
mitteln (z.B.
-verteilten
Variable schon ab 61 Werten signifikant von einer gleichlangen Gauß-Verteilung.
Der Exzeß ist erst ab 406 Werten signifikant zu unterscheiden.
Daraus muß geschlossen werden, daß die Analyse von Zeitreihen gleitender
Varianzen nicht mit der Methode der kleinsten Quadrate durchgeführt werden
kann, denn man muß einerseits über einen möglichst großen Zeitraum
mitteln (z.B. 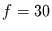 ), darf aber andererseits auch damit keine langen
Zeitreihen gleitender Varianzen erzeugen, da diese signifikant schief wären.
Daher kommt die
), darf aber andererseits auch damit keine langen
Zeitreihen gleitender Varianzen erzeugen, da diese signifikant schief wären.
Daher kommt die  -Verteilung für die Bearbeitung der Fragestellung
nicht in Frage. Die Schätzung der Varianz führt durch das Quadrieren zu
vielen sehr kleinen Werten und wenigen sehr großen.
Je länger der Mittelungszeitraum ist, desto eher wird dieser Effekt
weggemittelt, wodurch aber zeitlich lokale Information ebenso verlorengeht.
Wir benötigen demnach eine Variable, die mit zunehmenden Freiheitsgraden
rascher gegen die Gauß-Verteilung
konvergiert, als die
-Verteilung für die Bearbeitung der Fragestellung
nicht in Frage. Die Schätzung der Varianz führt durch das Quadrieren zu
vielen sehr kleinen Werten und wenigen sehr großen.
Je länger der Mittelungszeitraum ist, desto eher wird dieser Effekt
weggemittelt, wodurch aber zeitlich lokale Information ebenso verlorengeht.
Wir benötigen demnach eine Variable, die mit zunehmenden Freiheitsgraden
rascher gegen die Gauß-Verteilung
konvergiert, als die  -Verteilung. Da, wie wir gesehen haben, die
Schiefe der
-Verteilung. Da, wie wir gesehen haben, die
Schiefe der  -Verteilung der limitierende Faktor ist, die wiederum
ein Resultat des Quadrierens ist, bietet es sich an die Wurzel aus der
-Verteilung der limitierende Faktor ist, die wiederum
ein Resultat des Quadrierens ist, bietet es sich an die Wurzel aus der
 -verteilten Variable zu untersuchen.
Die dadurch entstehende Variable ist die Standardabweichung,
die
-verteilten Variable zu untersuchen.
Die dadurch entstehende Variable ist die Standardabweichung,
die 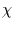 -verteilt ist.
Die Untersuchung der Konvergenz
der
-verteilt ist.
Die Untersuchung der Konvergenz
der 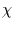 -Verteilung gegen die Gauß-Verteilung ist Inhalt des folgenden
Abschnitts.
-Verteilung gegen die Gauß-Verteilung ist Inhalt des folgenden
Abschnitts.


Nächste Seite: -Verteilung
Aufwärts: Zur zeitlichen Analyse von
Vorherige Seite: Transformation der Verteilungen
ich
2000-01-25