

Nächste Seite: Mindestens notwendige Fensterlängen
Aufwärts: Zur zeitlichen Analyse von
Vorherige Seite: -Verteilung
Eine 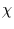 -verteilte Variable entsteht, wenn man die Wurzel einer
-verteilte Variable entsteht, wenn man die Wurzel einer
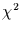 -verteilten Variable bildet. Da Varianzen
-verteilten Variable bildet. Da Varianzen 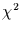 -verteilt sind,
sind Standardabweichungen
-verteilt sind,
sind Standardabweichungen 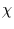 -verteilt.
Für die Transformation der Wahrscheinlichkeitsdichte folgt dann
nach Gleichung (2)
-verteilt.
Für die Transformation der Wahrscheinlichkeitsdichte folgt dann
nach Gleichung (2)
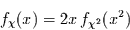 |
(20) |
und damit nach Gleichung(7)
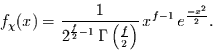 |
(21) |
Für das 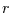 -te Moment folgt dann nach Gleichung (8)
-te Moment folgt dann nach Gleichung (8)
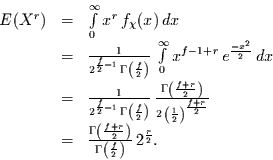 |
(22) |
Damit lassen sich für eine vorgegebene Anzahl von Freiheitsgraden4
die
Parameter Erwartungswert, Varianz, Schiefe und Exzeß berechnen. Erwartungswert
und Varianz können dazu verwendet werden, eine Gauß-Verteilung anzupassen.
Die Werte von Schiefe und Exzeß dienen dann als Maße für die Abweichung der
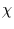 -Verteilung von der Gauß-Verteilung. Abbildung 3 zeigt
den Verlauf der Wahrscheinlichkeitsdichte der
-Verteilung von der Gauß-Verteilung. Abbildung 3 zeigt
den Verlauf der Wahrscheinlichkeitsdichte der 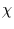 -Verteilung für
verschiedene Freiheitsgrade und die entsprechende Gauß-Verteilung.
-Verteilung für
verschiedene Freiheitsgrade und die entsprechende Gauß-Verteilung.
Abbildung:
Vergleich von 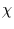 -Verteilung (durchgezogene Linie)
und Gauß-Verteilung (unterbrochene Linie)
mit gleichem Mittelwert und gleicher Varianz bei
1, 2, 3 und 10 Freiheitsgraden.
-Verteilung (durchgezogene Linie)
und Gauß-Verteilung (unterbrochene Linie)
mit gleichem Mittelwert und gleicher Varianz bei
1, 2, 3 und 10 Freiheitsgraden.
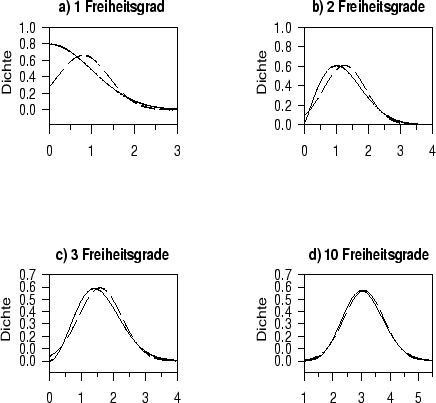 |
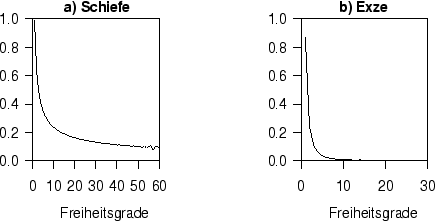
Abbildung 4 zeigt die Abhängigkeit von Schiefe und Exzeß von
der Anzahl der Freiheitsgrade 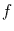 . Ein Vergleich von Abbildung 4
mit Abbildung 2 zeigt, daß tatsächlich, wie erwartet, die
Werte der Schiefe und des Exzesses bei einer
. Ein Vergleich von Abbildung 4
mit Abbildung 2 zeigt, daß tatsächlich, wie erwartet, die
Werte der Schiefe und des Exzesses bei einer 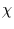 -verteilten Variable
mit zunehmender Anzahl der Freiheitsgrade schneller gegen null geht, als die
entsprechenden Werte einer
-verteilten Variable
mit zunehmender Anzahl der Freiheitsgrade schneller gegen null geht, als die
entsprechenden Werte einer 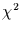 -verteilten Variable.
-verteilten Variable.
Abbildung:
a) Schiefe einer 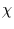 -verteilten Zufallsvariable
in Abhängigkeit von der Anzahl der Freiheitsgrade.
b) Exzeß einer
-verteilten Zufallsvariable
in Abhängigkeit von der Anzahl der Freiheitsgrade.
b) Exzeß einer 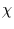 -verteilten Zufallsvariable
in Abhängigkeit von der Anzahl der Freiheitsgrade.
-verteilten Zufallsvariable
in Abhängigkeit von der Anzahl der Freiheitsgrade.
 |
Es stellt sich nun die Frage, wieviele Freiheitsgrade man mindestens zulassen
muß, damit Schiefe und Exzeß der 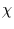 -Verteilung nicht signifikant von
null abweichen. Diese Frage ist gleichbedeutend damit, wie breit das
Datenfenster mindestens sein muß, das über die zu untersuchende Zeitreihe
geschoben wird, um die Zeitreihe der gleitenden
Standardabweichungen zu bilden.
Dieser Frage wird im nächsten Abschnitt nachgegangen.
-Verteilung nicht signifikant von
null abweichen. Diese Frage ist gleichbedeutend damit, wie breit das
Datenfenster mindestens sein muß, das über die zu untersuchende Zeitreihe
geschoben wird, um die Zeitreihe der gleitenden
Standardabweichungen zu bilden.
Dieser Frage wird im nächsten Abschnitt nachgegangen.


Nächste Seite: Mindestens notwendige Fensterlängen
Aufwärts: Zur zeitlichen Analyse von
Vorherige Seite: -Verteilung
ich
2000-01-25

