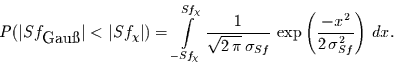

Nächste Seite: Zusammenfassung
Aufwärts: Zur zeitlichen Analyse von
Vorherige Seite: -Verteilung
Bei einer Gauß-Verteilung ist der Erwartungswert der Schiefe und des Exzesses
gleich null. Die Varianz dieser Größen hängt allerdings vom Datenumfang ab
(s. Gleichungen (13) und (14)). Schiefe und Exzeß
der  - und der
- und der 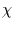 -Verteilung mit
-Verteilung mit 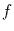 Freiheitsgraden
folgen aus den Gleichungen (15) und (22). Nun kann man
fragen, wie wahrscheinlich Schiefe und Exzeß einer
Verteilung von
Freiheitsgraden
folgen aus den Gleichungen (15) und (22). Nun kann man
fragen, wie wahrscheinlich Schiefe und Exzeß einer
Verteilung von 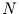 Realisationen
einer Gauß-verteilten Zufallsvariable einen mindestens so großen
Abstand von null haben,
wie Schiefe und Exzeß einer
vorgegebenen
Realisationen
einer Gauß-verteilten Zufallsvariable einen mindestens so großen
Abstand von null haben,
wie Schiefe und Exzeß einer
vorgegebenen  - bzw.
- bzw. 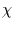 -Verteilung mit
-Verteilung mit 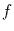 Freiheitsgraden. Unter der Annahme, daß Schiefe und Exzeß annähernd
Gauß-verteilt sind, folgt für die Wahrscheinlichkeit
Freiheitsgraden. Unter der Annahme, daß Schiefe und Exzeß annähernd
Gauß-verteilt sind, folgt für die Wahrscheinlichkeit
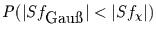 dafür, daß die Schiefe einer
Gauß-verteilten Variable näher an null ist,
als die der
dafür, daß die Schiefe einer
Gauß-verteilten Variable näher an null ist,
als die der 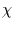 -verteilten Variable
-verteilten Variable
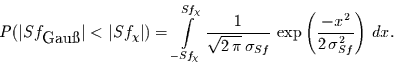 |
(23) |
Diese Gleichung gilt entsprechend auch für den Exzeß und für eine
 -verteilte Variable. Sie wird hier aber nur für den einen Fall
gelöst, da die Lösung auf die anderen Fälle übertragbar ist.
Um Gleichung (23) zu lösen, wird zunächst
die Schiefe der
-verteilte Variable. Sie wird hier aber nur für den einen Fall
gelöst, da die Lösung auf die anderen Fälle übertragbar ist.
Um Gleichung (23) zu lösen, wird zunächst
die Schiefe der 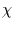 -Verteilung mit
-Verteilung mit 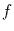 Freiheitsgraden
mit der Standardabweichung der Schiefe der Gauß-Verteilung normiert, d.h.
Freiheitsgraden
mit der Standardabweichung der Schiefe der Gauß-Verteilung normiert, d.h.
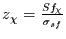 . Damit folgt
. Damit folgt
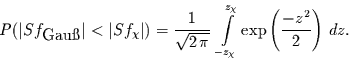 |
(24) |
Da das Integral über eine um null symmetrische Funktion gebildet wird,
folgt weiter
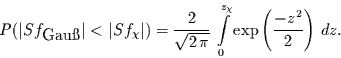 |
(25) |
Durch die Transformation
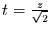 entsteht daraus
entsteht daraus
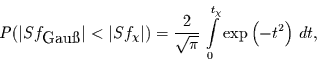 |
(26) |
was der Errorfunktion entspricht, so daß folgt
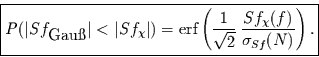 |
(27) |
Abbildung 5 zeigt die Wahrscheinlichkeit dafür, daß
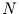 Realisationen einer Gauß-verteilten Variable zu einer Verteilung mit
einer betragsmäßig mindestens gleichgroßen Schiefe führen, wie eine
Realisationen einer Gauß-verteilten Variable zu einer Verteilung mit
einer betragsmäßig mindestens gleichgroßen Schiefe führen, wie eine
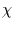 - bzw. eine
- bzw. eine  -Verteilung. Man sieht, daß die Schiefe der
-Verteilung. Man sieht, daß die Schiefe der
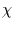 -Verteilung schon für wenige Freiheitsgrade nicht mehr signifikant
von der Schiefe der Gauß-Verteilung mit z.B. hundert Realisationen abweicht.
Bei der
-Verteilung schon für wenige Freiheitsgrade nicht mehr signifikant
von der Schiefe der Gauß-Verteilung mit z.B. hundert Realisationen abweicht.
Bei der  -Verteilung hingegen, ist die Schiefe selbst bei 30
Freiheitsgraden und sehr kurzen Reihen noch deutlich von der Schiefe
der Gauß-Verteilung zu unterscheiden.
-Verteilung hingegen, ist die Schiefe selbst bei 30
Freiheitsgraden und sehr kurzen Reihen noch deutlich von der Schiefe
der Gauß-Verteilung zu unterscheiden.
Abbildung:
Wahrscheinlichkeit 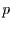 , mit der die Schiefe einer a)
, mit der die Schiefe einer a) 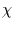 -verteilten
und b)
-verteilten
und b)  -verteilten Zufallsvariable stärker von null abweicht,
als bei
-verteilten Zufallsvariable stärker von null abweicht,
als bei 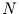 Realisationen einer Gauß-verteilten Zufallsvariable.
Realisationen einer Gauß-verteilten Zufallsvariable.
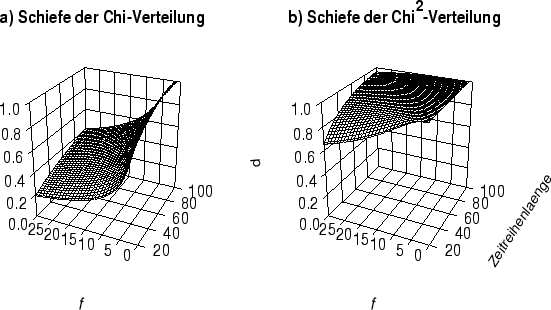 |
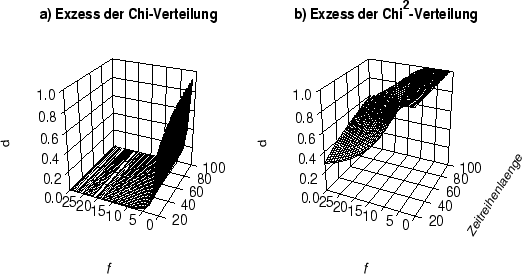
Abbildung 6 zeigt die Ergebnisse für die Untersuchung des
Exzesses. Auch hier sieht man die deutliche Überlegenheit der
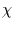 -Verteilung, auch wenn hier die
-Verteilung, auch wenn hier die  -Verteilung selbst kein
so fatales Bild abgibt, wie bei der Untersuchung der Schiefe.
-Verteilung selbst kein
so fatales Bild abgibt, wie bei der Untersuchung der Schiefe.
Abbildung:
Wahrscheinlichkeit 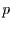 , mit der der Exzeß einer a)
, mit der der Exzeß einer a) 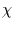 -verteilten
und b)
-verteilten
und b)  -verteilten Zufallsvariable stärker von null abweicht,
als bei
-verteilten Zufallsvariable stärker von null abweicht,
als bei 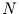 Realisationen einer Gauß-verteilten Zufallsvariable.
Realisationen einer Gauß-verteilten Zufallsvariable.
 |
Damit läßt sich sagen, daß sich gezeigt hat, daß eine Reihe
von gleitenden Standardabweichungen, auch wenn diese jeweils nur aus wenigen
Werten berechnet werden 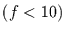 , nicht von einer Reihe Gauß-scher Zufallszahlen
zu unterscheiden ist, falls die Reihe der gleitenden Mittel nicht zu lang ist.
Nun kann man die Schiefe der
, nicht von einer Reihe Gauß-scher Zufallszahlen
zu unterscheiden ist, falls die Reihe der gleitenden Mittel nicht zu lang ist.
Nun kann man die Schiefe der 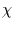 -Verteilung
-Verteilung 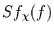 mit dem
90%-Signifikanzniveau
mit dem
90%-Signifikanzniveau
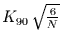 der Schiefe der Verteilung
von
der Schiefe der Verteilung
von 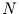 Gauß-verteilten Zufallszahlen gleichsetzen und nach
Gauß-verteilten Zufallszahlen gleichsetzen und nach 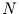 auflösen.
Man erhält
auflösen.
Man erhält
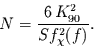 |
(28) |
Solange man keinen einfachen analytischen Ausdruck für
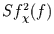 findet, kann man nicht die minimal notwendige Fensterlänge
findet, kann man nicht die minimal notwendige Fensterlänge 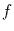 in Abhängigkeit
von der Länge der Datenreihe
in Abhängigkeit
von der Länge der Datenreihe 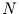 berechnen, wohl aber Glg. (28)
anwenden, und dann
berechnen, wohl aber Glg. (28)
anwenden, und dann 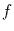 gegen
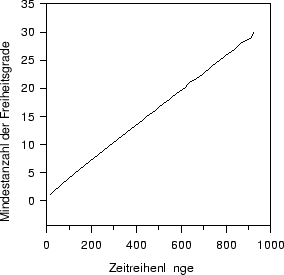
gegen 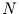 abbilden. Das Ergebnis ist in Abbildung
7 dargestellt und ist verblüffend einfach. Der linear erscheinende
Zusammenhang
abbilden. Das Ergebnis ist in Abbildung
7 dargestellt und ist verblüffend einfach. Der linear erscheinende
Zusammenhang 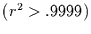 , spiegelt wider, daß die Schiefe der
, spiegelt wider, daß die Schiefe der 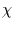 -Verteilung
proportional zu
-Verteilung
proportional zu 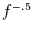 ist. Es folgt dann aus Abbildung 7
der Zusammenhang
ist. Es folgt dann aus Abbildung 7
der Zusammenhang
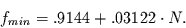 |
(29) |
Dabei stellt 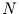 die Länge der Zeitreihe der gleitenden Standardabweichungen
dar. Diese folgt aus der Länge der Originalreihe
die Länge der Zeitreihe der gleitenden Standardabweichungen
dar. Diese folgt aus der Länge der Originalreihe 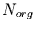 durch
durch
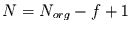 . Daraus folgt für die Anwendung
. Daraus folgt für die Anwendung
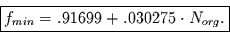 |
(30) |
Abbildung:
Minimal notwendige Fensterbreite 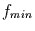 in Abhängigkeit
von der Zeitreihenlänge
für die Untersuchung gleitender Standardabweichungen.
in Abhängigkeit
von der Zeitreihenlänge
für die Untersuchung gleitender Standardabweichungen.
 |


Nächste Seite: Zusammenfassung
Aufwärts: Zur zeitlichen Analyse von
Vorherige Seite: -Verteilung
ich
2000-01-25