



Nächste Seite: Literatur
Aufwärts: Sukzessive und multiple Analysen
Vorherige Seite: Sukzessive Analysen
Inhalt
Bei den multiplen Analysen werden mehrere Einflußfaktoren simultan
betrachtet. Der Einfachheit halber werden in den hier untersuchten Beispielen
nur jeweils zwei Einflußfaktoren (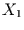 und
und 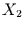 ) berücksichtigt.
Dabei können
) berücksichtigt.
Dabei können 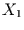 und
und 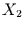 jeweils die Zeitreihen der
Sommermonatstemperaturen (
jeweils die Zeitreihen der
Sommermonatstemperaturen (
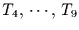 ) und der monatlichen
Sommerniederschläge (
) und der monatlichen
Sommerniederschläge (
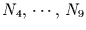 ), aber auch Quadrate
dieser Reihen sein. Gesucht wird nun nach
optimalen Anpassungen von zweidimensionalen Funktionen
), aber auch Quadrate
dieser Reihen sein. Gesucht wird nun nach
optimalen Anpassungen von zweidimensionalen Funktionen
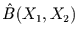 an die beobachtete Reihe der Jahrringbreiten
an die beobachtete Reihe der Jahrringbreiten 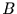 .
Es wurden drei Experimente mit verschiedenen vorgegebenen funktionalen
Zusammenhängen durchgeführt. Für jeden vorgegebenen Zusammenhang gibt es
bei zwei erlaubten Einflußfaktoren aus der Menge der zur Verfügung stehenden
klimatischen Zeitreihen eine bestimmte Anzahl an möglichen Kombinationen.
Davon ist wiederum nur ein gewisser Anteil signifikant. Die signifikanteste
Kombination wird selektiert und deren erklärte Varianz berechnet. Für die
drei durchgeführten Experimente ergeben sich dann folgende Ergebnisse:
.
Es wurden drei Experimente mit verschiedenen vorgegebenen funktionalen
Zusammenhängen durchgeführt. Für jeden vorgegebenen Zusammenhang gibt es
bei zwei erlaubten Einflußfaktoren aus der Menge der zur Verfügung stehenden
klimatischen Zeitreihen eine bestimmte Anzahl an möglichen Kombinationen.
Davon ist wiederum nur ein gewisser Anteil signifikant. Die signifikanteste
Kombination wird selektiert und deren erklärte Varianz berechnet. Für die
drei durchgeführten Experimente ergeben sich dann folgende Ergebnisse:
- Funktionaler Zusammenhang:
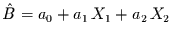
das erlaubt 66 Kombinationen, von denen 35 signifikant sind.
Signifikanteste Kombination:
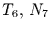
Erklärte Varianz:
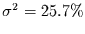
- Funktionaler Zusammenhang:
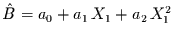
das erlaubt 12 Möglichkeiten, von denen 5 signifikant sind.
Signifikanteste Möglichkeit: 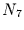
Erklärte Varianz:
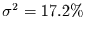
- Funktionaler Zusammenhang:
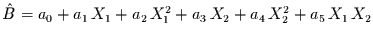
das erlaubt 78 Kombinationen, von denen 64 signifikant sind.
Signifikanteste Kombination: 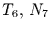
Erklärte Varianz:
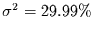
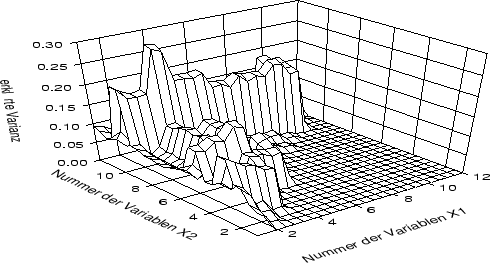
In Abb 4.12 ist die erklärte Varianz in Abhängigkeit von den zwei
verwendeten Einflußgrößen dargestellt. Man sieht deutlich, daß die
signifikanteste Kombination deutlich signifikanter ist als alle anderen
Kombinationen.
Abbildung:
Erklärte Varianzen multipler vollständiger
quadratischer Regressionen zwischen den klimatischen
Parametern für die Sommermonate in Potsdam (1 bis 6 = Monatstemperaturen
von April bis September, 7 bis 12 = monatliche Niederschlagssummen von
April bis September)
und der Jahrringbreite von Kiefern in
der Region Brandenburg von 1891 bis 1991.
 |
Das dritte Experiment stellt die Jahrringbreite als vollständige quadratische
Form von zwei Monatsmitteln klimatischer Einflußgrößen dar. Dieser Ansatz
repräsentiert eine Arbeitspunkthypothese, die besagt, daß es eine
bestimmte mittlere Niederschlagsmenge und eine bestimmte mittlere Temperatur
gibt, bei der das Wachstum optimal ist. Für alle anderen Kombinationen ist
(unter dieser Hypothese) das Wachstum schlechter. Diese Hypothese ist
durch einen Paraboloiden charakterisiert, der durch den Ansatz im dritten
Experiment erfaßt werden kann. Stellt man diesem Ansatz einen
aus sigmoiden Funktionen bestehenden Ansatz gegenüber,
so kann man testen, ob eine
alternative Hypothese (die der Sättigung) sinnvoller ist. Bei der
Sättigungshypothese geht man davon aus, daß das Baumwachstum in einem
bestimmten Intervall der klimatischen Einflußgrößen sensibel gegenüber
diesen ist, falls die klimatologischen Einflußgrößen aber eine obere
Schwelle überschreiten (bzw. eine unter Schwelle unterschreiten), keine
Abhängigkeit von diesen mehr besteht.
Untersuchungen zum Vergleich solcher verschiedener Hypothesen konnten im
zeitlichen Rahmen dieser Arbeit nicht mehr durchgeführt werden, sind aber
von besonderem Interesse. Zusätzlich können auch bei der multiplen
Betrachtung die Hauptkomponenten statt der Monatswerte als Einflußgrößen
verwendet werden.
In einem weiteren strategischen Entwicklungsschritt könnte man die
multiple und die sukzessive Herangehensweise koppeln, indem man sukzessive
die Dimension der multiplen Ansätze erhöht und dabei nach signifikant
besseren Zusammenhängen sucht. Auch dieser vielversprechenden Strategie
konnte im Rahmen dieser Arbeit nicht mehr nachgegangen werden.




Nächste Seite: Literatur
Aufwärts: Sukzessive und multiple Analysen
Vorherige Seite: Sukzessive Analysen
Inhalt
ich
2000-01-24
