Nächste Seite: Die Farben des Rauschens
Aufwärts: Prozesse mit langem Gedächtnis
Vorherige Seite: Spektren
Inhalt
Der ARFIMA(0,d,0)-Prozeß
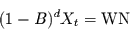 |
(17) |
mit 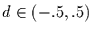 und WN=White Noise wird fraktionell
integrierter White-Noise-Prozeß oder einfach FIWN-Prozeß genannt.
In manchen Lehrbüchern (z.B. [14])
findet man auch die merkwürdige
Bezeichnung fraktionell differenzierter White-Noise-Prozeß (FDWN).
Der FIWN-Prozeß mit
und WN=White Noise wird fraktionell
integrierter White-Noise-Prozeß oder einfach FIWN-Prozeß genannt.
In manchen Lehrbüchern (z.B. [14])
findet man auch die merkwürdige
Bezeichnung fraktionell differenzierter White-Noise-Prozeß (FDWN).
Der FIWN-Prozeß mit 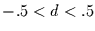 ist stationär. Er hat die AR
ist stationär. Er hat die AR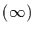 -Darstellung
-Darstellung
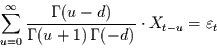 |
(18) |
und die MA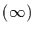 -Darstellung
-Darstellung
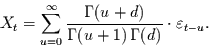 |
(19) |
Für 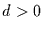 ist er ein Prozeß mit langem Gedächtnis. Dies kann man zeigen,
indem man die
ist er ein Prozeß mit langem Gedächtnis. Dies kann man zeigen,
indem man die 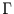 -Funktionen in Gleichung (19) mit der
Stirlingschen Formel approximiert. Die Koeffizienten in Gleichung
(19) verhalten sich dann für große
-Funktionen in Gleichung (19) mit der
Stirlingschen Formel approximiert. Die Koeffizienten in Gleichung
(19) verhalten sich dann für große 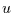 wie
wie 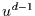 . Die Koeffizienten
der AR
. Die Koeffizienten
der AR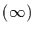 -Darstellung verhalten sich wie
-Darstellung verhalten sich wie 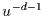 .
Das Spektrum des FIWN-Prozesses folgt aus Gleichung (15) zu
.
Das Spektrum des FIWN-Prozesses folgt aus Gleichung (15) zu
![\begin{displaymath}
S_{\mbox{FIWN}}(f) =\left[ 2\,\sin(\pi\,f) \right]^{-2d}\, \sigma_{\varepsilon}^{2}.
\end{displaymath}](img70.gif) |
(20) |
Man sieht sofort, daß für kleine Frequenzen die Approximation
![\begin{displaymath}
\lim\limits_{f\to 0} S_{\mbox{FIWN}}(f) =\left[ 2\,\pi\,f \right]^{-2d}\, \sigma_{\varepsilon}^{2}\sim f^{-2d}
\end{displaymath}](img71.gif) |
(21) |
gilt.
Da diese Näherung schon für 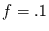 recht gut gilt (Fehler
recht gut gilt (Fehler 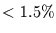 ),
bedeutet dies, daß man
in Beobachtungszeitreihen, die aus einem solchen Prozeß stammen,
für Wellenlängen von mehr als ca. zehn Zeitschritten ein
),
bedeutet dies, daß man
in Beobachtungszeitreihen, die aus einem solchen Prozeß stammen,
für Wellenlängen von mehr als ca. zehn Zeitschritten ein
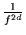 -Rauschen sieht.
Diese Erkenntnis ist zur Schätzung von
-Rauschen sieht.
Diese Erkenntnis ist zur Schätzung von 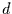 aus Daten wichtig.
In Abbildung 1 findet man das
FIWN-Spektrum nach Gleichung (20) und dessen Approximation nach
Gleichung (21).
aus Daten wichtig.
In Abbildung 1 findet man das
FIWN-Spektrum nach Gleichung (20) und dessen Approximation nach
Gleichung (21).
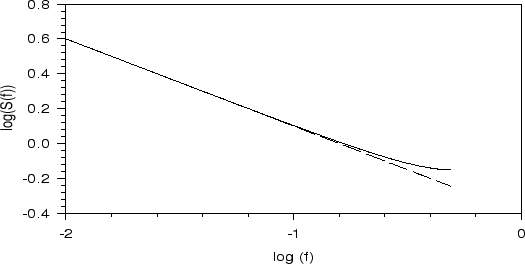
Abbildung 1:
Exaktes FIWN-Spektrum
(durchgezogene Linie) und dessen
Approximation durch ein 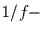 Spektrum (unterbrochene Linie).
Spektrum (unterbrochene Linie).
 |
Die Autokovarianzfunktion 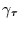 kann über das Parsevalsche Theorem
aus dem Spektrum wie folgt berechnet werden:
kann über das Parsevalsche Theorem
aus dem Spektrum wie folgt berechnet werden:
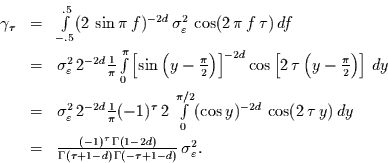 |
(22) |
Dabei wurde in der zweiten Zeile 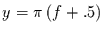 gesetzt und in der dritten
Zeile die Symmetrie des Integrals um
gesetzt und in der dritten
Zeile die Symmetrie des Integrals um 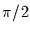 genutzt.
Für die Autokorrelationsfunktion
genutzt.
Für die Autokorrelationsfunktion 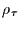 folgt daraus
folgt daraus
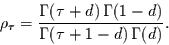 |
(23) |
Mit der Stirlingschen Approximation
und für große 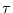 , sowie
, sowie 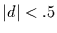 folgt dann
folgt dann
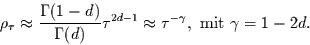 |
(24) |
Für 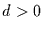 ist der Prozeß dann ein Prozeß mit langem Gedächtnis.
ist der Prozeß dann ein Prozeß mit langem Gedächtnis.




Nächste Seite: Die Farben des Rauschens
Aufwärts: Prozesse mit langem Gedächtnis
Vorherige Seite: Spektren
Inhalt
ich
2000-01-25