



Nächste Seite: Der FIWN-Prozeß
Aufwärts: Langes Gedächtnis
Vorherige Seite: Zusammenhang zu ARMA-Prozessen
Inhalt
Um das Spektrum eines ARFIMA-Prozesses zu berechnen, nutzt man seine
in Gleichung (8) ausgedrückte Eigenschaft,
ein linear gefilterter ARMA-Prozeß
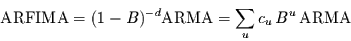 |
(9) |
zu sein.
Die Fouriertransformierte eines Filters
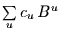 ist gegeben durch
ist gegeben durch
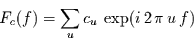 |
(10) |
und heißt Frequenzantwortfunktion oder Transferfunktion des Filters. Durch diese
Funktion ist es möglich, anzugeben, wie das Spektrum des Ausgangssignals
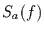 vom Spektrum des Eingangs
vom Spektrum des Eingangs 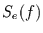 abhängt, es gilt nämlich die
für lineare Filter wichtige Beziehung
abhängt, es gilt nämlich die
für lineare Filter wichtige Beziehung
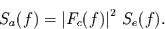 |
(11) |
Damit folgt für das Spektrum eines ARFIMA-Prozesses
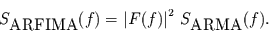 |
(12) |
Für den Differenzenfilter 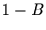 folgt die Transferfunktion
folgt die Transferfunktion
![\begin{displaymath}
\begin{array}{lcl}
F(f) & = & 1-\exp(i\,2\,\pi\,f)\\ [1ex]...
...4}\right)\right]
\,2\,\sin\left(\pi\,f\right),
\end{array}
\end{displaymath}](img55.gif) |
(13) |
deren Betrag gegeben ist durch
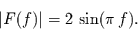 |
(14) |
Damit folgt für das ARFIMA-Spektrum aus Gleichung (12)
![\begin{displaymath}
S_{\mbox{ARFIMA}}(f) =\left[ 2\,\sin(\pi\,f) \right]^{-2d}\, S_{\mbox{ARMA}}(f).
\end{displaymath}](img57.gif) |
(15) |
Aus dieser Gleichung kann man entnehmen, daß das ARFIMA-Spektrum
für sehr kleine Frequenzen über alle Grenzen wächst, dann nämlich gilt
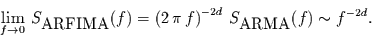 |
(16) |
Die Proportionalität der letzten Gleichung folgt daraus, daß für kleine
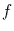 das Spektrum eines jeden ARMA-Prozesses konstant wird. Für die Analyse
von Zeitreihen spielt die Frage, ob sie ein
das Spektrum eines jeden ARMA-Prozesses konstant wird. Für die Analyse
von Zeitreihen spielt die Frage, ob sie ein 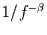 -Spektrum haben,
eine entscheidende Rolle.
-Spektrum haben,
eine entscheidende Rolle.




Nächste Seite: Der FIWN-Prozeß
Aufwärts: Langes Gedächtnis
Vorherige Seite: Zusammenhang zu ARMA-Prozessen
Inhalt
ich
2000-01-25
![\begin{displaymath}
\begin{array}{lcl}
F(f) & = & 1-\exp(i\,2\,\pi\,f)\\ [1ex]...
...4}\right)\right]
\,2\,\sin\left(\pi\,f\right),
\end{array}
\end{displaymath}](img55.gif)