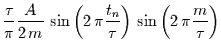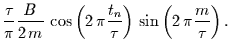

Nächste Seite: Veränderliche harmonische Anteile
Aufwärts: Einfluß der Mittelung auf
Vorherige Seite: Einfluß der Mittelung auf
Der Einfachheit halber betrachten wir zunächst eine einzige harmonische
Schwingung der Form
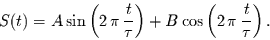 |
(5) |
Da die gefundenen Ergebnisse dann für jede beliebige harmonische Schwingung
gelten, kann das Ergebnis später verallgemeinert werden.
Einsetzen der Glg. (5) in Glg. (3) führt zu
![\begin{displaymath}
\begin{array}{rcl}
\overline{S(t_{n})} & = & \frac{1}{2\,m...
...,\pi\frac{t_{n}-m}{\tau}\right)\right]}_{\beta}.
\end{array}
\end{displaymath}](img19.gif) |
(6) |
Allgemein gilt
und
Damit folgt weiter
Für das zentrierte Mittel der Breite 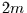 um den Zeitpunkt
um den Zeitpunkt 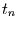 folgt dann
folgt dann
![\begin{displaymath}
\overline{S(t_{n})}=
\frac{\tau}{2\,\pi\,m}\,\sin\left(2\...
...) +
B \cos\left(2\,\pi\,\frac{t_{n}}{\tau}\right)
\right].
\end{displaymath}](img27.gif) |
(9) |
Ein Vergleich mit Glg. (5) zeigt, daß das gleitende Mittel einer
harmonischen Schwingung wieder eine harmonische Schwingung mit der gleichen
Phasenlage aber mit einer anderen (gedämpften)
Amplitude ergibt. Die Amplitude ist
um den Faktor
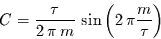 |
(10) |
geringer
als bei der ungemittelten Schwingung.
Man kann damit von jeder in gemittelten Daten gefundenen Schwingung
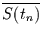 mit der Beziehung
mit der Beziehung
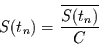 |
(11) |
auf die Schwingung 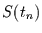 in der zeitkontinuierlichen Variable schließen.
Da für Mittelungsintervalle, die
klein gegenüber der Periode der Schwingung sind,
in der zeitkontinuierlichen Variable schließen.
Da für Mittelungsintervalle, die
klein gegenüber der Periode der Schwingung sind,
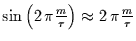 gilt, folgt
gilt, folgt
Das bedeutet, daß Schwingungen mit einer Periode, die wesentlich größer ist
als das Mittelungsintervall nicht nur in ihrer Phasenlage, sondern auch in
ihrer Amplitude unverändert bleiben.
Man beachte, daß Glg. (10) für beliebige Mittelungsintervalle gilt.
Daraus folgt, daß eine zeitkontinuierliche harmonische Schwingung
durch Tagesmittelwerte und durch Monatsmittelwerte mit der entsprechenden
Dämpfung ausgedrückt werden kann. Bezeichnet man den
Amplitudendämpfungsfaktor bei Monatsmitteln mit 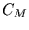 und den von
Tagesmitteln mit
und den von
Tagesmitteln mit 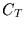 , so erhält man den Amplitudenfaktor zur Umrechnung
von Monatsmitteln auf Tagesmittel
, so erhält man den Amplitudenfaktor zur Umrechnung
von Monatsmitteln auf Tagesmittel 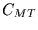 mit
mit
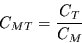 |
(12) |
und es folgt
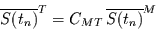 |
(13) |
In Abbildung 1 ist der Amplitudendämpfungsfaktor 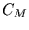 für einen
Mittelungszeitraum von einem Tag und einem Monat (30 Tagen)
für Schwingungen mit Perioden zwischen einem
Tag und einem Jahr dargestellt.
für einen
Mittelungszeitraum von einem Tag und einem Monat (30 Tagen)
für Schwingungen mit Perioden zwischen einem
Tag und einem Jahr dargestellt.
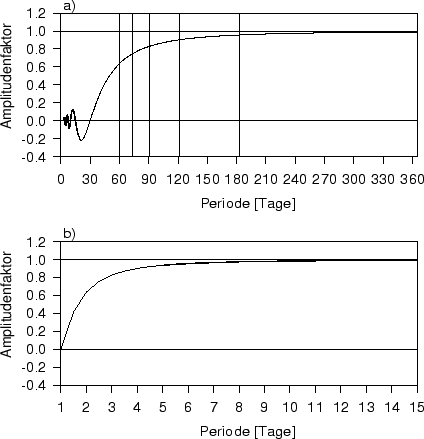
Abbildung:
Abhängigkeit der Amplitudendämpfung bei
a) dreißigtägiger Mittelung
einer harmonischen Schwingung mit Perioden zwischen
einem Tag und einem Jahr (die dünnen senkrechten Linien repräsentieren die
möglichen Oberschwingungen des Jahresgangs, die von Monatsdaten aufgelöst
werden können) und b) eintägiger Mittelung einer harmonischen
Schwingung mit Perioden zwischen einem Tag und 15 Tagen.
 |
Entsprechend der Abbildung 1 kann 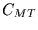 für Perioden
größer als 2 Wochen durch
für Perioden
größer als 2 Wochen durch
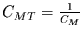 mit einem Fehler kleiner
mit einem Fehler kleiner
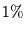 approximiert werden. Für Perioden größer als ein Jahr kann
approximiert werden. Für Perioden größer als ein Jahr kann 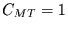 gesetzt werden. Die Amplitude wird dann um weniger als ein Prozent
unterschätzt.
Die gemittelten Schwingungen sind bis jetzt wie die ungemittelten
Schwingungen in kontinuierlicher Zeit
ausgedrückt worden.
Bei der Betrachtung von Monatsmitteln, wird diese Zeitfunktion
nun zu diskreten Zeitpunkten abgetastet, sodaß eine Zeitreihe entsteht.
Wegen des Abtasttheorems können dann nur noch Schwingungen mit Perioden
größer als zwei Monate, also
gesetzt werden. Die Amplitude wird dann um weniger als ein Prozent
unterschätzt.
Die gemittelten Schwingungen sind bis jetzt wie die ungemittelten
Schwingungen in kontinuierlicher Zeit
ausgedrückt worden.
Bei der Betrachtung von Monatsmitteln, wird diese Zeitfunktion
nun zu diskreten Zeitpunkten abgetastet, sodaß eine Zeitreihe entsteht.
Wegen des Abtasttheorems können dann nur noch Schwingungen mit Perioden
größer als zwei Monate, also 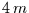 , untersucht werden.
Das bedeutet, daß einerseits harmonische Anteile des Jahresgangs, die eine
größere Periode als zwei Monate aufweisen, unter Berücksichtigung des
Amplitudendämpfungsfaktors
, untersucht werden.
Das bedeutet, daß einerseits harmonische Anteile des Jahresgangs, die eine
größere Periode als zwei Monate aufweisen, unter Berücksichtigung des
Amplitudendämpfungsfaktors 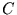 (s. Glg (10))
von Monatsdaten auf Tagesdaten
übertragen werden können. Andererseits können höherfrequente Anteile
des Jahresgangs nicht durch die Monatsdaten ausgedrückt werden. Solche
Anteile gehen, falls sie überhaupt in der Realität vorkommen,
durch die Mittelung verloren.
Die Zusammenhänge, die in diesem Abschnitt besprochen wurden, sind unabhängig
davon mit welcher Methode signifikante harmonische Anteile in den gemittelten
Daten gesucht wurden (z.B. Fourier-Analyse, Autokorrelationsspektralanalyse,
gleitende Fourier-Analyse, Wavelet-Analyse).
(s. Glg (10))
von Monatsdaten auf Tagesdaten
übertragen werden können. Andererseits können höherfrequente Anteile
des Jahresgangs nicht durch die Monatsdaten ausgedrückt werden. Solche
Anteile gehen, falls sie überhaupt in der Realität vorkommen,
durch die Mittelung verloren.
Die Zusammenhänge, die in diesem Abschnitt besprochen wurden, sind unabhängig
davon mit welcher Methode signifikante harmonische Anteile in den gemittelten
Daten gesucht wurden (z.B. Fourier-Analyse, Autokorrelationsspektralanalyse,
gleitende Fourier-Analyse, Wavelet-Analyse).


Nächste Seite: Veränderliche harmonische Anteile
Aufwärts: Einfluß der Mittelung auf
Vorherige Seite: Einfluß der Mittelung auf
ich
2000-01-24
![\begin{displaymath}
\begin{array}{rcl}
\overline{S(t_{n})} & = & \frac{1}{2\,m...
...,\pi\frac{t_{n}-m}{\tau}\right)\right]}_{\beta}.
\end{array}
\end{displaymath}](img19.gif)