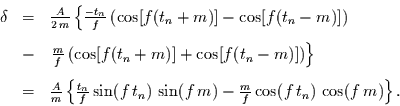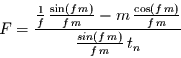

Nächste Seite: Quadratische Amplitudenfunktion
Aufwärts: Veränderliche harmonische Anteile
Vorherige Seite: Veränderliche harmonische Anteile
Eine harmonische Schwingung mit linearen Amplitudenfunktionen kann geschrieben werden
als
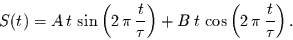 |
(14) |
Zunächst wird die Kreisfrequenz
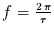 eingeführt,
woraus die handlichere Schreibweise
eingeführt,
woraus die handlichere Schreibweise
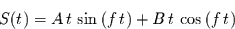 |
(15) |
folgt.
Dann gilt für das Mittel
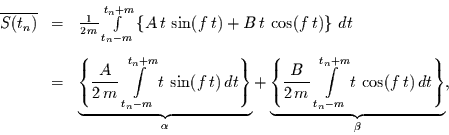 |
(16) |
mit
![\begin{displaymath}
\begin{array}{rcl}
\alpha & = &
\frac{A}{2\,m}
\left[
...
...}-m}{f}(\cos[f\,(t_{n}-m)])
\right\}}_{\delta}.
\end{array}
\end{displaymath}](img53.gif) |
(17) |
Und 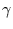 ist
ist
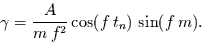 |
(18) |
Für 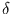 folgt
folgt
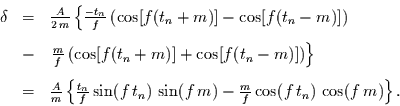 |
(19) |
Dann folgt für 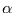
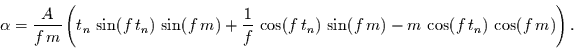 |
(20) |
Analog folgt für 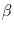
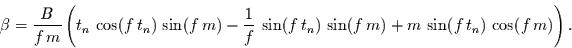 |
(21) |
Damit folgt für
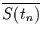
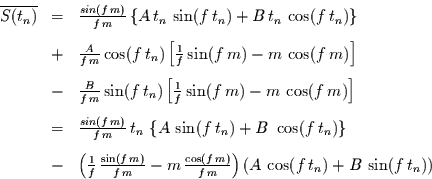 |
(22) |
Der erste Term stellt die Originalschwingung dar, wobei der für
gemittelte harmonische Schwingungen übliche Vorfaktor auftritt. Dieser ist
für Schwingungen mit einer Periode 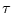 größer als das doppelte
Mittelungsintervall (
größer als das doppelte
Mittelungsintervall (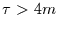 ) schon über .6. Mit zunehmender Wellenlänge
verschwindet dieser Dämpfungseinfluß.
Der zweite Term stellt eine Schwingung mit konstanter Amplitude dar, die
sich um den Faktor
) schon über .6. Mit zunehmender Wellenlänge
verschwindet dieser Dämpfungseinfluß.
Der zweite Term stellt eine Schwingung mit konstanter Amplitude dar, die
sich um den Faktor
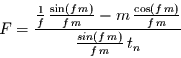 |
(23) |
von der Schwingung des ersten Terms unterscheidet. Wegen 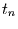 im Nenner
stirbt dieser Term mit zunehmender Zeit aus (der relative Fehler geht gegen
null). Für beliebig niedrige Frequenzen, bzw. beliebig kurze
Mittelungsintervalle folgt
im Nenner
stirbt dieser Term mit zunehmender Zeit aus (der relative Fehler geht gegen
null). Für beliebig niedrige Frequenzen, bzw. beliebig kurze
Mittelungsintervalle folgt
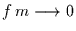 und der zweite Term in
Glg. (22)
verschwindet. Im ungünstigsten Fall ist
und der zweite Term in
Glg. (22)
verschwindet. Im ungünstigsten Fall ist 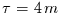 und es folgt
und es folgt
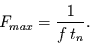 |
(24) |
Mit
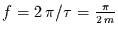 folgt dann
folgt dann
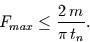 |
(25) |
Nun kann 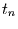 aber nur ein ganzes Vielfaches von
aber nur ein ganzes Vielfaches von 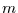 sein
(
sein
(
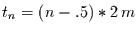 mit
mit 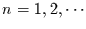 )
und es folgt
)
und es folgt
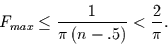 |
(26) |
Der zweite Term ist also immer kleiner als der erste Term.


Nächste Seite: Quadratische Amplitudenfunktion
Aufwärts: Veränderliche harmonische Anteile
Vorherige Seite: Veränderliche harmonische Anteile
ich
2000-01-24
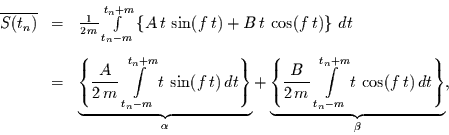
![\begin{displaymath}
\begin{array}{rcl}
\alpha & = &
\frac{A}{2\,m}
\left[
...
...}-m}{f}(\cos[f\,(t_{n}-m)])
\right\}}_{\delta}.
\end{array}
\end{displaymath}](img53.gif)