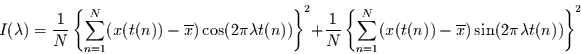


Nächste Seite: Anwendungen
Aufwärts: Spektrale Dichte
Vorherige Seite: Detrenden
Inhalt
Es kann vorkommen, daß eine vorliegende Zeitreihe aus nicht äquidistant
gemessenen Werten besteht (z.B. weil ein Meßgerät einen Eintrag sammelt,
bis das Sammelgefäß irgendwann voll ist). Auch dann kann ein Periodogramm
berechnet werden. Dies geschieht in diesem Fall
einfach über eine Regressionsanpassung
von Sinus- und Kosinusfunktionen. Man erhält so einen einfachen und anderen
Zugang zum Stichprobenspektrum als auf Seite ![[*]](crossref.gif) , indem man
eine Kleinstquadrateanpassung macht. Dazu wählt man zunächst das
System von anzupassenden Funktionen
, indem man
eine Kleinstquadrateanpassung macht. Dazu wählt man zunächst das
System von anzupassenden Funktionen 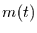 .
Dies sind sinnvollerweise Sinus- und
Kosinusfunktionen, bei den Fourier-Perioden:
.
Dies sind sinnvollerweise Sinus- und
Kosinusfunktionen, bei den Fourier-Perioden:
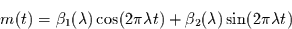 |
(1.26) |
Diese werden an die mittelwertbereinigte Zeitreihe durch folgenden
Ansatz optimal angepaßt:
![\begin{displaymath}
\sum_{t} [(x(t)-\overline{x})-m(t)]^{2} = \min
\end{displaymath}](img135.gif) |
(1.27) |
Leitet man diesen nach
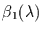 und
und
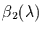 ab,
so erhält man die beiden Bedingungsgleichungen für diese. Für
das Periodogramm folgt dann (bei
ab,
so erhält man die beiden Bedingungsgleichungen für diese. Für
das Periodogramm folgt dann (bei 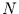 durchnummerierten Werten):
durchnummerierten Werten):
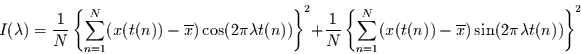 |
(1.28) |



Nächste Seite: Anwendungen
Aufwärts: Spektrale Dichte
Vorherige Seite: Detrenden
Inhalt
ich
2000-01-25
![[*]](crossref.gif) , indem man
eine Kleinstquadrateanpassung macht. Dazu wählt man zunächst das
System von anzupassenden Funktionen
, indem man
eine Kleinstquadrateanpassung macht. Dazu wählt man zunächst das
System von anzupassenden Funktionen