


Nächste Seite: Alterungsprozesse
Aufwärts: Nichtkonstante Ereigniswahrscheinlichkeitsdichten
Vorherige Seite: Nichtkonstante Ereigniswahrscheinlichkeitsdichten
Inhalt
Falls die Ereigniswahrscheinlichkeitsdichte 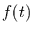 keine Konstante ist, bekommt
die Zeit eine explizite Bedeutung. Man kann zwischen stetigen
und unstetigen
keine Konstante ist, bekommt
die Zeit eine explizite Bedeutung. Man kann zwischen stetigen
und unstetigen 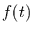 unterscheiden. Für stetige
unterscheiden. Für stetige 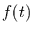 können theoretisch immer alle Fragen, die für den Poisson-Prozeß lösbar
sind, auch gelöst werden.
In der Praxis kann das sehr aufwendig sein, so daß
man numerische Näherungen bevorzugen könnte. Hier sollen nun allgemeine
Ausdrücke für die Wahrscheinlichkeit
können theoretisch immer alle Fragen, die für den Poisson-Prozeß lösbar
sind, auch gelöst werden.
In der Praxis kann das sehr aufwendig sein, so daß
man numerische Näherungen bevorzugen könnte. Hier sollen nun allgemeine
Ausdrücke für die Wahrscheinlichkeit 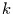 Ereignisse im Intervall
Ereignisse im Intervall 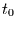 bis
bis 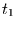 und für die Wartezeit auf das nächste Ereignis formuliert werden.
In den Abschnitten 2.2.2 bis 2.2.4 werden dann
Spezialfälle besprochen.
Um die Wahrscheinlichkeit zu finden, daß
und für die Wartezeit auf das nächste Ereignis formuliert werden.
In den Abschnitten 2.2.2 bis 2.2.4 werden dann
Spezialfälle besprochen.
Um die Wahrscheinlichkeit zu finden, daß 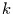 Ereignisse
im Intervall von
Ereignisse
im Intervall von 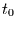 bis
bis 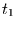 stattfinden, benötigen wir wieder die Lösungen der
Mastergleichung, deren allgemeine Formulierung gegeben ist durch
stattfinden, benötigen wir wieder die Lösungen der
Mastergleichung, deren allgemeine Formulierung gegeben ist durch
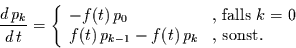 |
(2.17) |
Für stetige 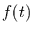 hat dieses Differentialgleichungssystem immer eindeutige
Lösungen. Die allgemeinen Lösungen der inhomogenen Gleichungen folgen als
Summe
aus deren allgemeinen homogenen Lösungen und jeweils
einer speziellen inhomogenen
Lösung, die durch Variation der Konstanten
aus den jeweiligen allgemeinen Lösungen der homogenen
Gleichungen gefunden werden können.
Das bedeutet, daß man im obigen Fall zunächst die allgemeine
Lösung der homogenen Gleichung für
hat dieses Differentialgleichungssystem immer eindeutige
Lösungen. Die allgemeinen Lösungen der inhomogenen Gleichungen folgen als
Summe
aus deren allgemeinen homogenen Lösungen und jeweils
einer speziellen inhomogenen
Lösung, die durch Variation der Konstanten
aus den jeweiligen allgemeinen Lösungen der homogenen
Gleichungen gefunden werden können.
Das bedeutet, daß man im obigen Fall zunächst die allgemeine
Lösung der homogenen Gleichung für 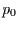
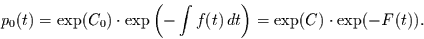 |
(2.18) |
angibt und die Anfangsbedingung
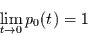 |
(2.19) |
einflechtet. Diese Anfangsbedingung bedeutet, daß die Wahrscheinlichkeit, kein
Ereignis im Intervall von 0 bis  vorzufinden gegen 1 geht, wenn die
Intervallänge gegen 0 geht. Dann ist
vorzufinden gegen 1 geht, wenn die
Intervallänge gegen 0 geht. Dann ist 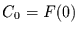 und es folgt die Lösung der
homogenen Differentialgleichung unter Berücksichtigung der Anfangsbedingungen
zu
und es folgt die Lösung der
homogenen Differentialgleichung unter Berücksichtigung der Anfangsbedingungen
zu
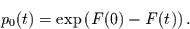 |
(2.20) |
Für 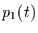 gilt dann nach Gleichung (2.17)
die inhomogene Differentialgleichung
gilt dann nach Gleichung (2.17)
die inhomogene Differentialgleichung
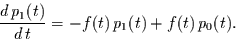 |
(2.21) |
Dabei ist der zweite Term auf der rechten Seite der inhomogene Anteil der DGL.
An dieser Stelle muß die Lösung der DGL für 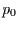 eingesetzt werden.
Die allgemeine
Lösung des homogenen Anteils von Gleichung (2.21) ist analog
zu Gleichung (2.20) gegeben durch
eingesetzt werden.
Die allgemeine
Lösung des homogenen Anteils von Gleichung (2.21) ist analog
zu Gleichung (2.20) gegeben durch
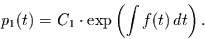 |
(2.22) |
Aus der Variation der Konstanten (d.h. setze Gleichung (2.22) mit
dem Ansatz
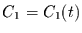 in die inhomogene Differentialgleichung ein) folgt dann
die Differentialgleichung für
in die inhomogene Differentialgleichung ein) folgt dann
die Differentialgleichung für 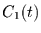
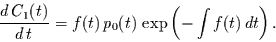 |
(2.23) |
Daraus ist 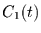 durch Integration bestimmbar.
Es ist leicht einsichtig, daß das Lösungsverfahren sehr langatmig und für
große
durch Integration bestimmbar.
Es ist leicht einsichtig, daß das Lösungsverfahren sehr langatmig und für
große 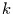 auch sehr aufwendig werden kann, denn zur Lösung der
auch sehr aufwendig werden kann, denn zur Lösung der 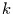 -ten DGL
muß die Lösung der
-ten DGL
muß die Lösung der 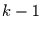 -ten DGL bekannt sein und als inhomogener Term
eingesetzt werden. Deshalb werden solche Probleme gerne mit Hilfe von
Markov-Ketten gelöst.
Einfacher ist die Frage nach der Wartezeitverteilung, d.h. nach der
Wahrscheinlichkeit, das man wenn man ab dem Zeitpunkt
-ten DGL bekannt sein und als inhomogener Term
eingesetzt werden. Deshalb werden solche Probleme gerne mit Hilfe von
Markov-Ketten gelöst.
Einfacher ist die Frage nach der Wartezeitverteilung, d.h. nach der
Wahrscheinlichkeit, das man wenn man ab dem Zeitpunkt 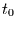 wartet,
bis
wartet,
bis 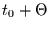 warten muß, bis das erste Ereignis stattfindet.
Dazu darf erstens im Zeitintervall
warten muß, bis das erste Ereignis stattfindet.
Dazu darf erstens im Zeitintervall 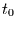 bis
bis 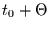 kein Ereignis
stattfinden, während zweitens
im Intervall
kein Ereignis
stattfinden, während zweitens
im Intervall 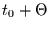 bis
bis
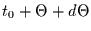 ein Ereignis stattfinden muß. Die Wartezeitwahrscheinlichkeitsdichte
ein Ereignis stattfinden muß. Die Wartezeitwahrscheinlichkeitsdichte
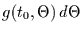 ist dann das Produkt der
Wahrscheinlichkeit, daß zwischen
ist dann das Produkt der
Wahrscheinlichkeit, daß zwischen 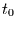 und
und 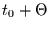 kein Ereignis
stattfindet
kein Ereignis
stattfindet
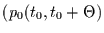 aus Gleichung (2.20)) mit der Wahrscheinlichkeitsdichte
dafür, daß zwischen
aus Gleichung (2.20)) mit der Wahrscheinlichkeitsdichte
dafür, daß zwischen 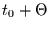 und
und
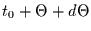 ein Ereignis
stattfindet (
ein Ereignis
stattfindet (
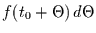 ).
Damit gilt für die Wartezeitverteilungsdichte
).
Damit gilt für die Wartezeitverteilungsdichte
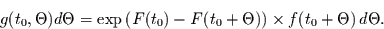 |
(2.24) |
Ein Vergleich von Gleichung (2.24) und den Gleichungen (2.22)
und (2.23) zeigt, daß die Wartezeitverteilung
eine wesentlich einfacher
zugängliche Größe ist, als die Wahrscheinlichkeitsverteilung
für beliebige 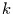 Ereignisse im Zeitraum von
Ereignisse im Zeitraum von 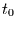 bis
bis 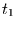 .
Die Wahrscheinlichkeit, daß man, wenn man ab dem Zeitpunkt
.
Die Wahrscheinlichkeit, daß man, wenn man ab dem Zeitpunkt 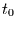 auf ein
Ereignis wartet, höchstens die Zeit
auf ein
Ereignis wartet, höchstens die Zeit 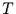 warten muß, folgt dann zu
warten muß, folgt dann zu
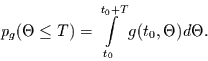 |
(2.25) |
Diese Größe wird in der Extremwertstatistik Risiko genannt. Sie gibt an,
wie groß das Risiko ist, in der ab 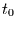 folgenden Zeitspanne
folgenden Zeitspanne 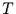 ein
Ereignis zu haben.
ein
Ereignis zu haben.
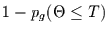 ist dann die Wahrscheinlichkeit dafür, daß man mindestens
so lange warten muß.
In den folgenden Abschnitten werden einige
einfache aber nützliche Beispiele explizit besprochen.
ist dann die Wahrscheinlichkeit dafür, daß man mindestens
so lange warten muß.
In den folgenden Abschnitten werden einige
einfache aber nützliche Beispiele explizit besprochen.



Nächste Seite: Alterungsprozesse
Aufwärts: Nichtkonstante Ereigniswahrscheinlichkeitsdichten
Vorherige Seite: Nichtkonstante Ereigniswahrscheinlichkeitsdichten
Inhalt
ich
2000-01-24