


Nächste Seite: Wie erkennt man stochastische
Aufwärts: Stochastische Zusammenhänge zweier Zufallsvariablen
Vorherige Seite: Einleitung
Inhalt
Man kann sich leicht vorstellen, daß man von 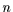 Menschen sowohl ihre Körpergröße
Menschen sowohl ihre Körpergröße
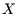 , als auch ihr Gewicht
, als auch ihr Gewicht 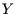 mißt. Weiterhin kann man sich leicht vorstellen, daß
diese beiden Größen nicht unabhängig voneinander sind. Die Abhängigkeit gilt aber
nur im Mittel, denn man kann zwar erwarten, daß eine große Person schwerer ist als
ein kleine, aber das Umgekehrte ist im Einzelfall immer möglich. In diesem Beispiel,
wo man den Zusammenhang sofort einsieht, braucht man natürlich nicht mehr zu testen,
ob die Daten einen Zusammenhang suggerieren, sondern kann gleich nach dessen
Stärke und nach optimalen Approximationen dieses Zusammenhangs fragen. Anders
sieht die Situation aus wenn man als Wissenschaftler Neuland betritt, d.h. nach
Zusammenhängen sucht, wo man nicht von vornherein weiß, daß zumindest
stochastisch ein Zusammenhang besteht. Zunächst müssen wir klar sehen, was mit
stochastischem Zusammenhang gemeint ist. Die wichtigste Einschränkung, die hier
gemacht wird, ist, daß die Realisationen von
mißt. Weiterhin kann man sich leicht vorstellen, daß
diese beiden Größen nicht unabhängig voneinander sind. Die Abhängigkeit gilt aber
nur im Mittel, denn man kann zwar erwarten, daß eine große Person schwerer ist als
ein kleine, aber das Umgekehrte ist im Einzelfall immer möglich. In diesem Beispiel,
wo man den Zusammenhang sofort einsieht, braucht man natürlich nicht mehr zu testen,
ob die Daten einen Zusammenhang suggerieren, sondern kann gleich nach dessen
Stärke und nach optimalen Approximationen dieses Zusammenhangs fragen. Anders
sieht die Situation aus wenn man als Wissenschaftler Neuland betritt, d.h. nach
Zusammenhängen sucht, wo man nicht von vornherein weiß, daß zumindest
stochastisch ein Zusammenhang besteht. Zunächst müssen wir klar sehen, was mit
stochastischem Zusammenhang gemeint ist. Die wichtigste Einschränkung, die hier
gemacht wird, ist, daß die Realisationen von 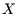 und
und 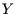 nur paarweise untersucht
werden, d.h. daß jeder Realisation von
nur paarweise untersucht
werden, d.h. daß jeder Realisation von 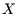 genau ein
genau ein 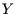 zugeordnet wird und
umgekehrt. Bei dem oben gegebenen Beispiel ist das klar: einer Messung ist eine
Realisierung von einer Körpergröße und einem Gewicht zugeordnet. Ganz anders ist
es aber z.B. bei einer Zeitreihe, die die Realisation des folgenden Prozesses ist:
zugeordnet wird und
umgekehrt. Bei dem oben gegebenen Beispiel ist das klar: einer Messung ist eine
Realisierung von einer Körpergröße und einem Gewicht zugeordnet. Ganz anders ist
es aber z.B. bei einer Zeitreihe, die die Realisation des folgenden Prozesses ist:
Bei diesem Prozess gibt es einen deterministischen Zusammenhang zwischen 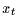 ,
,
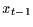 und
und 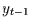 und einen zwischen
und einen zwischen 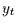 und
und 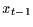 und
und 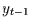 . Damit
hängen sowohl
. Damit
hängen sowohl 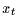 als auch
als auch 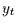 von der gemeinsamen Vergangenheit ab. Sie
hängen damit also von den vorhergehenden Werten der Zeitreihen selbst ab. Demnach
ist die Information
über den Zusammenhang vollständig
in den Zeitreihen vorhanden.
Bei der Analyse von Paaren der Art
von der gemeinsamen Vergangenheit ab. Sie
hängen damit also von den vorhergehenden Werten der Zeitreihen selbst ab. Demnach
ist die Information
über den Zusammenhang vollständig
in den Zeitreihen vorhanden.
Bei der Analyse von Paaren der Art 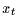 und
und 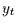 muß er aber nicht
sichtbar werden.
Da der Prozess rekursiv ist, liegt ein Teil der Information
über die Realisation von
muß er aber nicht
sichtbar werden.
Da der Prozess rekursiv ist, liegt ein Teil der Information
über die Realisation von 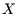 zur Zeit
zur Zeit 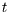 möglicherweise (das hängt von der konkreten Gestalt von
möglicherweise (das hängt von der konkreten Gestalt von 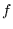 und
und 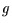 ab)
in der Realisation von
ab)
in der Realisation von 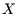 und/oder
und/oder 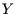 zu viel früheren Zeiten. Die Dynamik könnte
konkret so aussehen, daß man in einer endlichen Realisatin (Zeitreihe)
keine signifikante
stochastische Abhängigkeit zu irgendeinem der
vorherigen Werte der beiden Variablen finden kann. Man muß dann die Variablen
stochastisch unabhängig nennen. Das zeigt, daß stochastische Unabhängigkeit nicht
ausschließt, daß die beobachteten Größen sogar völlig deterministisch voneinander
abhängen.
Nach dieser Warnung nun zur konkreten Definition von stochastischer Unabhängigkeit:
Wir betrachten
zu viel früheren Zeiten. Die Dynamik könnte
konkret so aussehen, daß man in einer endlichen Realisatin (Zeitreihe)
keine signifikante
stochastische Abhängigkeit zu irgendeinem der
vorherigen Werte der beiden Variablen finden kann. Man muß dann die Variablen
stochastisch unabhängig nennen. Das zeigt, daß stochastische Unabhängigkeit nicht
ausschließt, daß die beobachteten Größen sogar völlig deterministisch voneinander
abhängen.
Nach dieser Warnung nun zur konkreten Definition von stochastischer Unabhängigkeit:
Wir betrachten 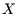 und
und 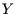 als Zufallsvariable, da es für uns zunächst zufällig
erscheint ob große oder kleine Werte realisiert werden. Die Frage ist nun, ob die
Wahrscheinlichkeit dafür, daß für die Variable
als Zufallsvariable, da es für uns zunächst zufällig
erscheint ob große oder kleine Werte realisiert werden. Die Frage ist nun, ob die
Wahrscheinlichkeit dafür, daß für die Variable
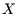 der Zahlenwert
der Zahlenwert 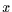 realisiert wird, davon
abhängt, daß für das zugeordnete
realisiert wird, davon
abhängt, daß für das zugeordnete 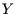 der Wert
der Wert 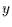 realisiert wird. Diese bedingte
Wahrscheinlichkeit [2] nennen wir
realisiert wird. Diese bedingte
Wahrscheinlichkeit [2] nennen wir 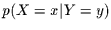 oder kürzer
oder kürzer 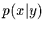 . Falls die Realisation
von
. Falls die Realisation
von 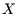 nicht von der Realisation von
nicht von der Realisation von 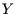 abhängt, muß gelten:
abhängt, muß gelten:
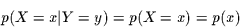 |
(1) |
und umgekehrt auch
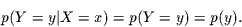 |
(2) |
Dabei stellen die Terme ganz rechts wieder nur verkürzte Schreibweisen dar.
Die nächste wichtige Größe ist die Wahrscheinlichkeit dafür, daß das
Verbundereignis 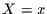 und
und 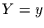 eintritt. Diese Verbundwahrscheinlichkeit nennen wir
eintritt. Diese Verbundwahrscheinlichkeit nennen wir
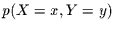 , oder kurz
, oder kurz 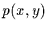 . Man kann sich nun durch kurzes
Überlegen klar
machen, daß bei stochastischer Unabhängigkeit, d.h. wenn die Gleichungen
(1) und (2) gelten, die Verbundwahrscheinlichkeit
. Man kann sich nun durch kurzes
Überlegen klar
machen, daß bei stochastischer Unabhängigkeit, d.h. wenn die Gleichungen
(1) und (2) gelten, die Verbundwahrscheinlichkeit 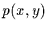 gleich dem
Produkt der Einzelwahrscheinlichkeiten
gleich dem
Produkt der Einzelwahrscheinlichkeiten 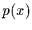 und
und 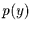 sein muß.
Kennt man also die Verbundwahrscheinlichkeit und die Einzelwahrscheinlichkeiten, so
kann man die stochastische Unabhängigkeit sofort erkennen. Nun ist es aber so, daß
man diese im allgemeinen nicht kennt, sondern schätzen muß. Selbst wenn man sie
wüßte, gäbe es noch das Problem, daß eine endliche Realisierung immer auch durch
Zufall mal ein sehr seltenes Ereignis sein kann. Der im nächsten Abschnitt vorgestellte
Test, berechnet nun gerade, wie unwahrscheinlich das geschätzte
sein muß.
Kennt man also die Verbundwahrscheinlichkeit und die Einzelwahrscheinlichkeiten, so
kann man die stochastische Unabhängigkeit sofort erkennen. Nun ist es aber so, daß
man diese im allgemeinen nicht kennt, sondern schätzen muß. Selbst wenn man sie
wüßte, gäbe es noch das Problem, daß eine endliche Realisierung immer auch durch
Zufall mal ein sehr seltenes Ereignis sein kann. Der im nächsten Abschnitt vorgestellte
Test, berechnet nun gerade, wie unwahrscheinlich das geschätzte 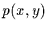 unter der
Annahme
unter der
Annahme
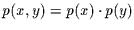 ist.
ist.
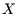 und
und 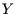 können dabei sehr verschiedene Arten von Zufallsvariablen sein. Z.B.
können die Variablen nominal skaliert sein, wie es bei
können dabei sehr verschiedene Arten von Zufallsvariablen sein. Z.B.
können die Variablen nominal skaliert sein, wie es bei 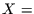 Farbe des Apfels und
Farbe des Apfels und
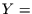 Geschmack des Apfels der Fall wäre. Sie müssen nur in disjunkte Klassen
eingeteilt sein, d.h. ein Apfel kann nicht gleichzeitig grün und rot sein. Die Variablen
können auch ordinal skaliert sein, wie es zum Beispiel die Wettereinteilung in sehr
schlecht über mittel bis sehr gut ist.
In diesem Fall ist eine
Klasseneinteilung vorgegeben. Hat man metrische Variablen, z.B. Körpergröße in
Geschmack des Apfels der Fall wäre. Sie müssen nur in disjunkte Klassen
eingeteilt sein, d.h. ein Apfel kann nicht gleichzeitig grün und rot sein. Die Variablen
können auch ordinal skaliert sein, wie es zum Beispiel die Wettereinteilung in sehr
schlecht über mittel bis sehr gut ist.
In diesem Fall ist eine
Klasseneinteilung vorgegeben. Hat man metrische Variablen, z.B. Körpergröße in
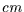 oder Temperaturen in
oder Temperaturen in 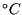 , so muß man diese selbst in Ereignisklassen
einteilen und daraus die Wahrscheinlichkeit für das Eintreten eines Ereignisses einer
bestimmten Klasse schätzen.
Zum Schluß dieses Abschnittes soll nicht unerwähnt bleiben, daß man das Konzept
der stochastischen Abhängigkeit bei Zeitreihen auch selbstbezüglich und
über Kreuz
anwenden kann. Man erhält dann stochastische Auto-Abhängigkeit bzw.
stochastische Kreuzabhängigkeit.
, so muß man diese selbst in Ereignisklassen
einteilen und daraus die Wahrscheinlichkeit für das Eintreten eines Ereignisses einer
bestimmten Klasse schätzen.
Zum Schluß dieses Abschnittes soll nicht unerwähnt bleiben, daß man das Konzept
der stochastischen Abhängigkeit bei Zeitreihen auch selbstbezüglich und
über Kreuz
anwenden kann. Man erhält dann stochastische Auto-Abhängigkeit bzw.
stochastische Kreuzabhängigkeit.



Nächste Seite: Wie erkennt man stochastische
Aufwärts: Stochastische Zusammenhänge zweier Zufallsvariablen
Vorherige Seite: Einleitung
Inhalt
ich
2000-01-25