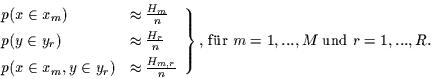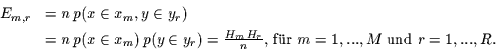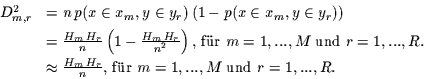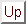


Nächste Seite: Wie stark ist ein
Aufwärts: Stochastische Zusammenhänge zweier Zufallsvariablen
Vorherige Seite: Was bedeutet stochastische Unabhängigkeit?
Inhalt
Um stochastische Abhängigkeit zu erkennen, muß man zunächst die
Hypothese stochastischer Unabhängigkeit aufstellen und dann testen,
ob man diese Hypothese auf hohem Niveau ablehnen kann [1].
Dazu definiert man
zuerst die Nullhypothese, nämlich daß die zwei Zufallsvariablen
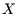 und
und 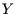 stochastisch unabhängig sind. Wenn dem so ist, muß
für die bedingten Wahrscheinlichkeiten
stochastisch unabhängig sind. Wenn dem so ist, muß
für die bedingten Wahrscheinlichkeiten 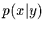 und
und 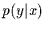 gelten:
gelten:
also auch
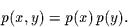 |
(3) |
Diese Wahrscheinlichkeitsdichten sind nicht bekannt, können aber geschätzt
werden. Dies geschieht durch Klasseneinteilung und die Kontingenztafel.
Teilen wir also zunächst allgemein die Variable 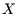 in
in 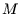 Klassen und die
Variable
Klassen und die
Variable 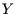 in
in 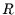 Klassen ein. Diese Einteilung sollte so gewählt sein,
daß in jeder Klasse mindestens 5 Werte liegen [5]. Die Klassen müssen aber
auf jeden Fall disjunkt sein. Die Wahrscheinlichkeiten aus Gleichung
(3) können nun über die absoluten Häufigkeiten
Klassen ein. Diese Einteilung sollte so gewählt sein,
daß in jeder Klasse mindestens 5 Werte liegen [5]. Die Klassen müssen aber
auf jeden Fall disjunkt sein. Die Wahrscheinlichkeiten aus Gleichung
(3) können nun über die absoluten Häufigkeiten 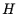 dieser
zweidimensionalen Klasseneinteilung bestimmt werden. Es wird also geschätzt:
dieser
zweidimensionalen Klasseneinteilung bestimmt werden. Es wird also geschätzt:
Falls die Nullhypothese (d.h. Glg. (3)) richtig ist,
dann ist die Antwort auf die Frage wieviel der insgesamt 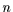 Realisierungen in der Klasse
Realisierungen in der Klasse 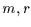 liegen, durch ein Bernoulli-Experiment
gegeben.
liegen, durch ein Bernoulli-Experiment
gegeben.
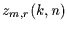 ist dann die Zufallsvariable, die angibt, wie wahrscheinlich
(unter der Bedingung der Nullhypothese)
ist dann die Zufallsvariable, die angibt, wie wahrscheinlich
(unter der Bedingung der Nullhypothese) 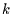 von
von 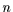 Realisierungen in der
Klasse
Realisierungen in der
Klasse 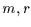 liegen. Diese Variable ist binomial-verteilt mit dem
Erwartungswert
liegen. Diese Variable ist binomial-verteilt mit dem
Erwartungswert 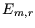 :
:
Für die zugehörige Varianz 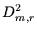 gilt dann:
gilt dann:
Die normierte Variable von 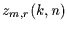 ist dann für große
ist dann für große 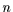 näherungsweise normalverteilt, d.h.
näherungsweise normalverteilt, d.h.
Damit ist die Summe der Quadrate dieser Normierten von 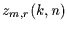 eine
eine
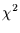 -verteilte Variable:
-verteilte Variable:
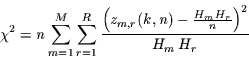 |
(4) |
Diese 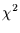 -verteilte Zufallsvariable hat die folgenden Freiheitsgrade.
Da es
-verteilte Zufallsvariable hat die folgenden Freiheitsgrade.
Da es 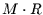 Klassen gibt ergibt dies schon mal
Klassen gibt ergibt dies schon mal 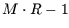 Freiheitsgrade.
Die Anzahl der Freiheiten verringert sich jedoch um
Freiheitsgrade.
Die Anzahl der Freiheiten verringert sich jedoch um 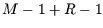 , da die
Wahrscheinlichkeiten
, da die
Wahrscheinlichkeiten 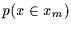 und
und 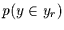 jeweils bis auf
einen Wert (der sich ergibt, weil die Summe
jeweils bis auf
einen Wert (der sich ergibt, weil die Summe 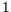 sein muß) geschätzt werden
mußten. Damit ist der Freiheitsgrad der
sein muß) geschätzt werden
mußten. Damit ist der Freiheitsgrad der 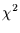 -Verteilung
-Verteilung 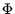 gegeben
durch:
gegeben
durch:
Nun kann man mit Hilfe von Gleichung (4) testen, wie wahrscheinlich
die vorliegende Realisation unter der Annahme der Nullhypothese ist. Dazu
muß man nur für 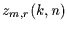 in Gleichung (4) die absolute
beobachtete Häufigkeit
in Gleichung (4) die absolute
beobachtete Häufigkeit 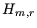 einsetzen. Wenn der damit berechnete Wert
einsetzen. Wenn der damit berechnete Wert
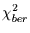 einen zu einem bestimmten Signifikanzniveau vorgegebenen
Wert überschreitet, dann ist es auf diesem Niveau unwahrscheinlich, daß
die Nullhypothese wahr ist.
Das Programm zus.for (s. Anhang C)
geht noch einen Schritt weiter und berechnet
zu
einen zu einem bestimmten Signifikanzniveau vorgegebenen
Wert überschreitet, dann ist es auf diesem Niveau unwahrscheinlich, daß
die Nullhypothese wahr ist.
Das Programm zus.for (s. Anhang C)
geht noch einen Schritt weiter und berechnet
zu
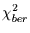 den genauen Wert des Signifikanzniveaus.
den genauen Wert des Signifikanzniveaus.



Nächste Seite: Wie stark ist ein
Aufwärts: Stochastische Zusammenhänge zweier Zufallsvariablen
Vorherige Seite: Was bedeutet stochastische Unabhängigkeit?
Inhalt
ich
2000-01-25
![\begin{displaymath}
\begin{array}{ll}
p(x\vert y) & = p(x)\\ [1ex]
p(y\vert x) & = p(y)\\
\end{array}
\end{displaymath}](img30.gif)
![\begin{displaymath}
\begin{array}{ll}
p(x\vert y) & = p(x)\\ [1ex]
p(y\vert x) & = p(y)\\
\end{array}
\end{displaymath}](img30.gif)