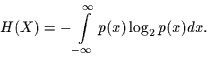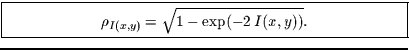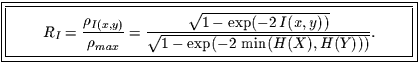


Nächste Seite: Welcher Art ist ein
Aufwärts: Stochastische Zusammenhänge zweier Zufallsvariablen
Vorherige Seite: Wie erkennt man stochastische
Inhalt
Um die Stärke eines stochastischen Zusammenhangs zu messen, stehen
verschiedene Maße zur Verfügung. So werden in den
Numerical Recipies [4] ein Continigenzkoeffizient und Cramer's 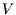 angegeben. Sie sind beide zwischen null und eins skaliert, aber können
nicht objektiv gewertet werden. Auf der anderen Seite gibt es bedingte
Maße, wie den Pearson Korrelationskoeffizient [5],
dessen Quadrat angibt,
welcher Anteil der Varianz der Variablen durch einen linearen Zusammenhang
erfaßt werden kann. Spearman und Kendall geben ähnliche Koeffizienten an,
die für monotone Zusammenhänge gelten [4].
Im Folgenden soll nun ein Maß aus der Informationstheorie [3]
verwendet werden,
daß die Stärke eines Zusammenhangs angibt, ohne auf Bedingungen wie
Linearität oder Monotonie angewiesen zu sein [6].
Ausgangspunkt ist dabei die in einer Zufallsvariablen enthaltene Information
angegeben. Sie sind beide zwischen null und eins skaliert, aber können
nicht objektiv gewertet werden. Auf der anderen Seite gibt es bedingte
Maße, wie den Pearson Korrelationskoeffizient [5],
dessen Quadrat angibt,
welcher Anteil der Varianz der Variablen durch einen linearen Zusammenhang
erfaßt werden kann. Spearman und Kendall geben ähnliche Koeffizienten an,
die für monotone Zusammenhänge gelten [4].
Im Folgenden soll nun ein Maß aus der Informationstheorie [3]
verwendet werden,
daß die Stärke eines Zusammenhangs angibt, ohne auf Bedingungen wie
Linearität oder Monotonie angewiesen zu sein [6].
Ausgangspunkt ist dabei die in einer Zufallsvariablen enthaltene Information
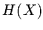 , die gegeben ist durch:
, die gegeben ist durch:
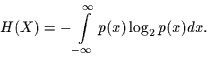 |
(5) |
Hat man nun eine Stichprobe bzw. eine Zeitreihe (oder eine Variable),
diskret skaliert ist, so geht das Integral in die Summe über die relativen
Klassenhäufigkeiten über:
Hat man es nun mit zwei Stichproben zu tun, die keine gleichartige Information
enthalten, so gilt
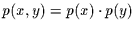 und die Information beider
Stichproben zusammengenommen
ist die Summe der Einzelinformationen. Andernfalls, d.h. falls die
Stichproben
und die Information beider
Stichproben zusammengenommen
ist die Summe der Einzelinformationen. Andernfalls, d.h. falls die
Stichproben 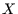 und
und 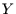 gleichartige Information enthalten, ist die gemeinsame
Information
gleichartige Information enthalten, ist die gemeinsame
Information 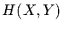 geringer
als die Summe der Einzelinformationen. Der Betrag um den
die gemeinsame Information geringer ist, heißt Transinformation
geringer
als die Summe der Einzelinformationen. Der Betrag um den
die gemeinsame Information geringer ist, heißt Transinformation 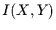 zwischen
zwischen 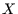 und
und 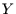 . Demnach gilt:
. Demnach gilt:
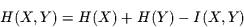 |
(6) |
Theoretisch können die Informationen alle Werte zwischen null und 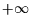 annehmen. Es werden nun verschiedene Normierungen verwendet, um daraus
relative Maße zu machen. In der Literatur findet man die folgenden
Normierungen gewöhnlich alle unter dem Namen Redundanz
annehmen. Es werden nun verschiedene Normierungen verwendet, um daraus
relative Maße zu machen. In der Literatur findet man die folgenden
Normierungen gewöhnlich alle unter dem Namen Redundanz 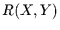 :
:
- Wenn man sich dafür interessiert, wie hoch der Anteil der Transinformation
an der Information der Stichprobe
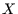 ist, definiert man sinnvoll:
ist, definiert man sinnvoll:
- Wenn man sich dafür interessiert, wie hoch der Anteil der Transinformation
an der Information der Stichprobe
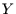 ist, definiert man sinnvoll:
ist, definiert man sinnvoll:
- Interessiert man sich für die maximale Redundanz, so kann man definieren:
- Interessiert man sich für die mittlere Redundanz, so setzt man die
mittlere Information der Stichproben ein:
Zwar sind alle diese Maße zwischen null und eins beschränkt, aber nicht
geeignet um sie mit anderen Maßen (insbesondere dem
Pearson-Korrelationskoeffizient) zu vergleichen. Desweiteren sagt eine
Redundanz von z.B. 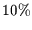 allein noch nicht viel aus.
Es soll nun der Zusammenhang zwischen der Information und den
Pearson-Korrelationskoeffizienten gezeigt werden, der es erlaubt, letztendlich
auf ein vergleichbares Maß zu kommen.
Zunächst kann aus den Gleichungen (5) und (6) die
folgende Gleichung für die Transinformation hergeleitet werden:
allein noch nicht viel aus.
Es soll nun der Zusammenhang zwischen der Information und den
Pearson-Korrelationskoeffizienten gezeigt werden, der es erlaubt, letztendlich
auf ein vergleichbares Maß zu kommen.
Zunächst kann aus den Gleichungen (5) und (6) die
folgende Gleichung für die Transinformation hergeleitet werden:
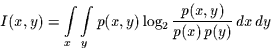 |
(7) |
Um nun den Zusammenhang zum Pearson-Korrelationskoeffizienten zu erhalten,
wird für 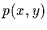 die zweidimensionale Gauß-Verteilung eingesetzt:
die zweidimensionale Gauß-Verteilung eingesetzt:
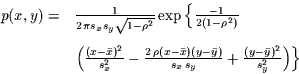 |
(8) |
mit
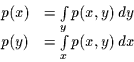 |
(9) |
Die Integration von Gleichung (7) unter Berücksichtigung von
Gleichung (8) und (9) führt auf folgenden Zusammenhang:
Stellt man diesen Zusammenhang nach 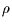 um, so erhält man einen
Kontingenzkoeffizienten, der aus der Information abgeleitet ist, und im
Fall eines linearen Zusammenhangs gleich dem
Pearson-Korrelationskoeffizienten ist:
Diese Gleichung bildet die Transinformation, die theoretisch Werte zwischen
null und unendlich annehmen kann auf das Intervall null bis eins ab. In der
Praxis ist die Transinformation aber durch den kleineren Werte von
um, so erhält man einen
Kontingenzkoeffizienten, der aus der Information abgeleitet ist, und im
Fall eines linearen Zusammenhangs gleich dem
Pearson-Korrelationskoeffizienten ist:
Diese Gleichung bildet die Transinformation, die theoretisch Werte zwischen
null und unendlich annehmen kann auf das Intervall null bis eins ab. In der
Praxis ist die Transinformation aber durch den kleineren Werte von 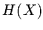 und
und 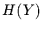 beschränkt. Deshalb wird
beschränkt. Deshalb wird 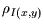 noch weiter normiert,
in dem es auf diesen maximal möglichen Wert bezogen wird. Man erhält dann
für die informationstheoretische Kontingenz
noch weiter normiert,
in dem es auf diesen maximal möglichen Wert bezogen wird. Man erhält dann
für die informationstheoretische Kontingenz 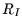 folgenden Zusammenhang:
Nun kann man zu
folgenden Zusammenhang:
Nun kann man zu 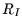 auch die Signifikanz ausrechnen. Dazu stellt man
erneut die Nullhypothese auf, daß
auch die Signifikanz ausrechnen. Dazu stellt man
erneut die Nullhypothese auf, daß 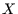 und
und 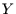 unabhängig sind, d.h., daß
unabhängig sind, d.h., daß
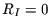 ist. Wenn
ist. Wenn 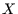 in
in 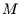 und
und 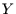 in
in 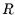 Klassen eingeteilt ist, dann
ist der Erwartungswert der Transinformation nur unter Berücksichtigiung der
Nullhypothese nur von den Freiheitsgraden dieser Klasseneinteilung abhängig.
Man erhält den Erwartungswert
Klassen eingeteilt ist, dann
ist der Erwartungswert der Transinformation nur unter Berücksichtigiung der
Nullhypothese nur von den Freiheitsgraden dieser Klasseneinteilung abhängig.
Man erhält den Erwartungswert 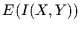 :
:
Nun ist
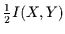 genau
genau 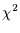 -verteilt mit
-verteilt mit
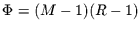 Freiheitsgraden. Dann gilt:
Freiheitsgraden. Dann gilt:
Mit dieser Gleichung läßt sich zu jedem berechneten Wert von 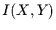 und
deshalb auch zu jedem Wert von
und
deshalb auch zu jedem Wert von 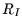 die zugehörige Signifikanz berechnen.
Bei der Berechnung der informationstheoretischen Maße ist zu beachten, daß
die Klasseneinteilung möglichst so gewählt werden sollte, daß die
Klassenhäufigkeiten in etwa gleichverteilt sind [6]. Dies ist im Gegensatz zu der
Einteilung, die man zweckmäßigerweise bei dem
die zugehörige Signifikanz berechnen.
Bei der Berechnung der informationstheoretischen Maße ist zu beachten, daß
die Klasseneinteilung möglichst so gewählt werden sollte, daß die
Klassenhäufigkeiten in etwa gleichverteilt sind [6]. Dies ist im Gegensatz zu der
Einteilung, die man zweckmäßigerweise bei dem 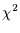 -Unabhängigkeitstest
macht.
-Unabhängigkeitstest
macht.



Nächste Seite: Welcher Art ist ein
Aufwärts: Stochastische Zusammenhänge zweier Zufallsvariablen
Vorherige Seite: Wie erkennt man stochastische
Inhalt
ich
2000-01-25