Ergebnisse der Hauptkomponentenanalyse

Als eine erste Anwendung der Hauptkomponentenanalyse werden die Temperatur- und Niederschlagszeitreihen der sechs Monate der Wachstumsperiode (April-September) hauptachsentransformiert. Die sich daraus ergebenden EOF sind in den Abbildungen 4.6 und 4.7 dargestellt. Nun kann man in einem nächsten Schritt die Hauptkomponenten der beiden Klimaelemente gemeinsam berechnen. Für die Wachstumsperiode bekommt man dann 12 gemeinsame Hauptkomponenten für Niederschlag und Temperatur. In Abbildung 4.8 sind diese 12 EOF in Abhängigkeit von den EOF der reinen Temperatur- bzw. Niederschlagsvariationen dargestellt. 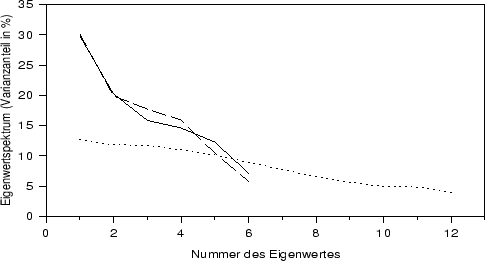Abbildung 4.9 zeigt für alle drei EOF-Zerlegungen das sogenannte Eigenwertspektrum, das angibt, wie sich die Varianz auf die einzelnen Hauptkomponenten verteilt. Man sieht, daß sowohl bei der Temperatur, als auch beim Niederschlag die erste EOF etwa 30 %, die ersten beiden EOF zusammen etwa 50 % der Varianz erklären. Die letzte EOF erklärt jeweils zwischen 6 % und 7% der Varianz, was nicht ohne weiteres vernachlässigbar erscheint. Die Eigenwerte der gemeinsamen Hauptkomponenten nehmen noch deutlich weniger steil ab, wie das bei den einzelnen Klimaelementen der Fall ist. Von den 12 Eigenwerten ist der erste schon unter 13%; der letze bei 4 %.

Abbildung: Empirische Orthogonalfunktionen der Sommermonatstemperaturen (April-September) von Potsdam für die Zeit von 1891 bis 1991.

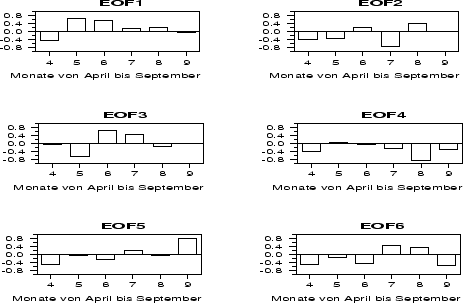Abbildung: Empirische Orthogonalfunktionen der Sommermonatsniederschläge (April-September) von Potsdam für die Zeit von 1891 bis 1991.

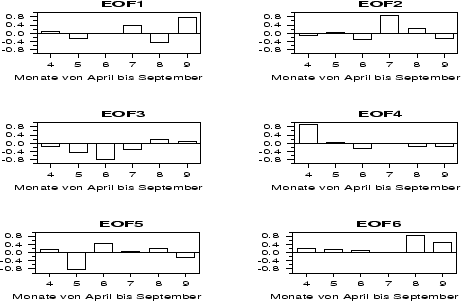Abbildung: Empirische Orthogonalfunktionen der Sommermonatstemperaturen und -niederschläge (April-September) von Potsdam für die Zeit von 1891 bis 1991 4.8.

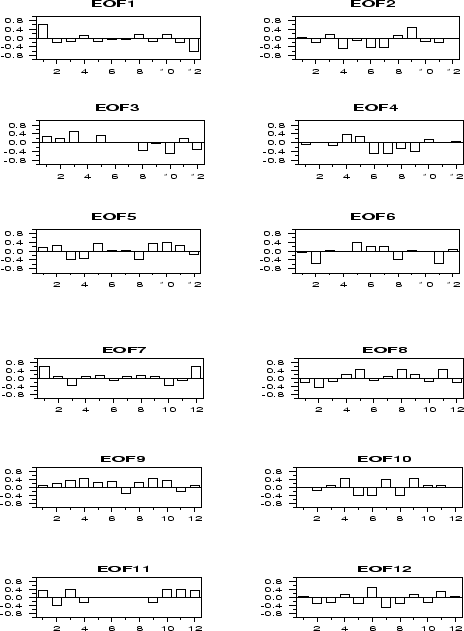Abbildung: Eigenwertspektren der EOF von Sommertemperaturen (durchgezogene Linie), Sommerniederschlägen (unterbrochene Linie) und der Kombination aus beidem (gepunktete Linie).

Im nächsten Schritt stellt sich nun die Frage, welche der Hauptkomponenten einen Zusammenhang mit der Zeitreihe der Jahrringbreiten zeigen. Dazu sind in den Abbildungen 4.10 und 4.11 die Zusammenhänge zwischen den PC-Zeitreihen der Temperatur und des Niederschlags einerseits (jeweils auf der Grundlage aller 12 Kalendermonate berechnet) und der Zeitreihe der Jahrringbreiten andererseits dargestellt. Dazu werden wieder die in Abschnitt 4.3.1 eingeführten Verfahren verwendet. Abb. 4.10 zeigt keinen signifikanten Zusammenhang zu irgendeiner Temperaturvariation des Vorjahres. Die erste EOF der Temperatur des Jahres des Baumrings wird ein hoch signifikanter nicht-linearer und nicht-monotoner Zusammenhang selektiert, der in einem Scatterdiagramm genauer untersucht werden sollte. Zur zweiten EOF der Temperatur besteht ein linearer und zur dritten wieder ein nicht-linearer und nicht-monotoner Zusammenhang. Auch für die zehnte, elfte und zwölfte EOF und einige EOF des Folgejahres findet man signifikante Zusammenhänge. Beim Niederschlag findet man zahlreiche lineare sowie nicht-lineare und nicht-monotone Zusammenhänge, die ein recht uneinheitliches Bild ergeben.

Abbildung: Oben: Verschiedene Maße des Zusammenhangs zwischen der Zeitreihe der Jahrringbreiten von Kiefern in Brandenburg und den EOF der monatlichen Mitteltemperaturen in Potsdam zwischen 1891 und 1991: Transinformation (dicke durchgezogene Linie), Pearson-Korrelation (dünne durchgezogene Linie), Spearman-Korrelation (dünne unterbrochene Linie) und Kendall-Korrelation (Strichpunktlinie). Unten: Verschiedene Signifikanzmaße: Quadrate 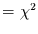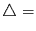$= \chi ^{2}$, $\bigtriangleup =$ Signifikanz der Spearman-Korrelation, 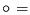$\circ =$ Signifikanz der Pearson-Korrelation und 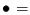$\bullet =$ Signifikanz der Transinformation.

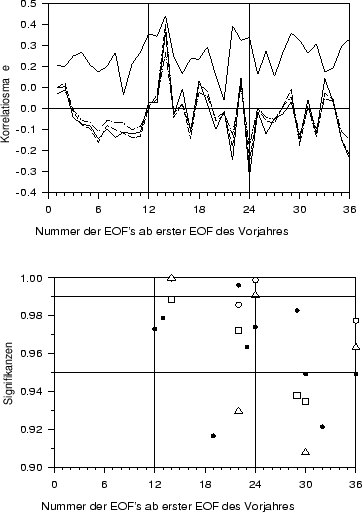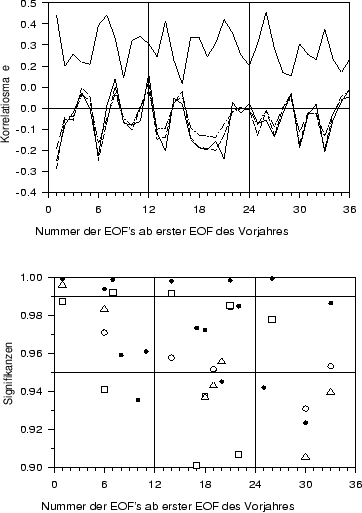
Abbildung: Oben: Verschiedene Maße des Zusammenhangs zwischen der Zeitreihe der Jahrringbreiten von Kiefern in Brandenburg und den EOF der monatlichen Niederschlagssummen in Potsdam zwischen 1891 und 1991: Transinformation (dicke durchgezogene Linie), Pearson-Korrelation (dünne durchgezogene Linie), Spearman-Korrelation (dünne unterbrochene Linie) und Kendall-Korrelation (Strichpunktlinie). Unten: Verschiedene Signifikanzmaße: Quadrate 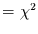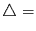$= \chi ^{2}$, $\bigtriangleup =$ Signifikanz der Spearman-Korrelation, 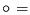$\circ =$ Signifikanz der Pearson-Korrelation und $\bullet =$ Signifikanz der Transinformation.