Exponentielles Altern

Für das exponentielle Altern kann man die Ereigniswahrscheinlichkeitsdichte

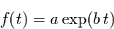$$f(t)= a \exp(b\,t)$$ (2.26)

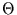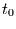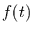wählen. Gefragt ist nun nach der Wahrscheinlichkeitsdichte dafür, eine Zeit $\Theta$ auf ein Ereignis warten zu müssen, wenn man zur Zeit $t_{0}$ mit der Beobachtung beginnt. Dazu müssen wir die Wahrscheinlichkeitsdichte $f(t)$ umformulieren für den Fall, daß ein Ereignis zur Zeit 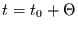$t=t_{0}+\Theta$ stattfindet. Es gilt

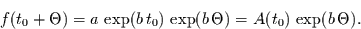$$f(t_{0}+\Theta)= a\, \exp(b\,t_{0}) \,\exp(b\,\Theta) = A(t_{0})\,\exp(b\,\Theta).$$ (2.27)

Die Formulierung ist demnach vom Anfangszeitpunkt der Beobachtung unabhängig, der Koeffizient vor der Exponentialfunktion hingegen nicht. Die Stammfunktion von 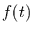$f(t)$ ist gegeben durch

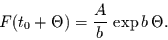$$F(t_{0}+\Theta)= \frac{A}{b}\,\exp{b\,\Theta}.$$ (2.28)

Damit folgt für die Wartezeitverteilungsdichte aus Gleichung (2.24)

$$\begin{array}{lcl} g(t_{0},\Theta) d\Theta & = & \exp\left... ...t_{0})}{b}[\exp(b\,\Theta)-1]\right]\,d\Theta. \end{array}$$ (2.29)

Nun kann der Begriff des Alterns auf zwei Arten verstanden werden. Einerseits kann die Wahrscheinlichkeit für das Eintreten eines Ereignisses zwischen zwei Ereignissen altern, um dann, wenn das Ereignis eingetreten ist wieder auf seinen Ursprungszustand zurückzufallen. Andererseits kann sich die Eintrittswahrscheinlichkeit unbeeindruckt davon, ob ein Ereignis stattfindet weiter entsprechend 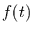$f(t)$ verhalten. Die erste Interpretation ist z.B. im Zusammenhang mit Vulkanen und Erdbeben von Bedeutung. Man kann mit einer gewissen Begründung annehmen, daß sich in einem Vulkan etwas anstaut, bis dieser ausbricht, wonach der Prozeß Zyklus erneut beginnt. Auf die gleiche Weise kann man sich vorstellen, daß die Schubspannung an Kontinentalplatten kontinuierlich zunimmt, bis sie eine Schwelle überschreitet, wodurch es zu einem Erdbeben kommt. Danach ist die Situation wieder völlig entspannt. Diese Interpretation von Gleichung (2.29) vereinfacht die Situation, für den Fall, daß man nach der Wahrscheinlichkeitsdichte für die Zeit zwischen zwei Ereignissen fragt. Dann ist 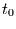$t_{0}$ nämlich immer null und 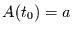$A(t_{0})=a$. Gleichung (2.29) reduziert sich dann zur Gompertz-Verteilung

$$g(t_{0},\Theta) d\Theta = a\,\exp\left[b\,\Theta- \frac{a}{b}[\exp(b\,\Theta)-1]\right]\,d\Theta$$ (2.30)

die gelegentlich auch als Gumbel-Verteilung bekannt ist. Bei der zweiten Interpretation von Gleichung (2.29) unterstellt man ein stochastisches System, das einen langfristigen exponentiellen Trend aufweist, der auf die Ereigniswahrscheinlichkeit wirkt. Dies kann z.B. durch einen exponentiellen externen Antrieb realisiert sein. Man könnte dies als Modellvorstellung für die mögliche Zunahme von Stürmen (und anderen extremen Ereignissen) durch den exponentiell ansteigenden anthropogenen Einfluß auf das Klima unterstellen.