


Nächste Seite: Zyklische Punktprozesse und stochastische
Aufwärts: Alterungsprozesse
Vorherige Seite: Exponentielles Altern
Inhalt
Für das Altern nach dem Potenzgesetz bietet sich der Ansatz
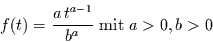 |
(2.31) |
an. Will man die Wartezeit wieder ab einem beliebigen Startpunkt 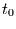 messen, so folgt
messen, so folgt
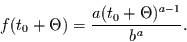 |
(2.32) |
Für die Stammfunktion gilt dann
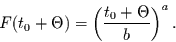 |
(2.33) |
Dies kann man in Gleichung (2.24) einsetzen und erhält die
Wartezeitverteilungsdichte
![\begin{displaymath}
g(t_{0}+\Theta) d\Theta=\frac{a}{b} \left(\frac{t_{0}+\Thet...
...ight)^{a} -
\left(\frac{t_{0}+\Theta}{b}\right)^{a}\right].
\end{displaymath}](img113.gif) |
(2.34) |
Für den Fall, das man sich nur für die Wartezeit zwischen zwei Ereignissen
(also unter klar vorgegebenen wenigen Startpunkten) interessiert und davon
ausgeht daß, nach jedem Ereignis die Zeit wieder bei 0 losläuft, d.h.
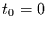 folgt die Weibull-Verteilung
folgt die Weibull-Verteilung
![\begin{displaymath}
g(\Theta) d\Theta=\frac{a}{b} \left(\frac{\Theta}{b}\right)...
...1}
\exp\left[ -
\left(\frac{\Theta}{b}\right)^{a}\right].
\end{displaymath}](img115.gif) |
(2.35) |
Die Wahrscheinlichkeit dafür, daß zwischen zwei Ereignissen weniger als
die Zeit 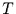 vergeht, ist bei einem solchen Prozeß gegeben durch
vergeht, ist bei einem solchen Prozeß gegeben durch
![\begin{displaymath}
p(\Theta\le T) = \int\limits_{t_{0}}^{t_{0}+T} g(t_{0},\The...
...
= 1-\exp\left[ -
\left(\frac{\Theta}{b}\right)^{a}\right].
\end{displaymath}](img116.gif) |
(2.36) |
Für 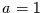 ist
ist 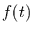 eine Konstante und somit geht die Betrachtung in den
Poisson-Prozeß über. Die Weibull-Verteilung muß dann in die
Exponentialverteilung übergehen. Das tut sie, wie man leicht sieht.
eine Konstante und somit geht die Betrachtung in den
Poisson-Prozeß über. Die Weibull-Verteilung muß dann in die
Exponentialverteilung übergehen. Das tut sie, wie man leicht sieht.



Nächste Seite: Zyklische Punktprozesse und stochastische
Aufwärts: Alterungsprozesse
Vorherige Seite: Exponentielles Altern
Inhalt
ich
2000-01-24
![\begin{displaymath}
p(\Theta\le T) = \int\limits_{t_{0}}^{t_{0}+T} g(t_{0},\The...
...
= 1-\exp\left[ -
\left(\frac{\Theta}{b}\right)^{a}\right].
\end{displaymath}](img116.gif)